Теорема об изменении количества движения
Количеством движения материальной точки называется векторная величина Количеством движения механической системы
Установим связь между количеством движения системы и скоростью центра масс механической системы. Возьмем производную по времени от обеих частей второго уравнения (3.10)
Сравнивая это уравнение с (3.23), получаем
Количество движения системы равно произведению массы системы на скорость ее центра масс. Докажем теорему об изменении количества движения материальной точки. Основной закон динамики точки (3.3) представим в виде
Пусть движущаяся точка имеет в момент времени
Величина
Изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени. Докажем эту теорему для механической системы. Возьмем от левой и правой частей (3.23) производные по времени:
Производная по времени от количества движения системы равна сумме действующих на систему внешних сил. Интегрируя уравнение (3.27), получим выражение теоремы в интегральной форме:
Изменение количества движения системы за некоторый промежуток времени равно сумме импульсов действующих на систему внешних сил за тот же промежуток времени.
|

 , равная произведению массы точки на вектор ее скорости. Направлен этот вектор так же, как и скорость точки, т.е. по касательной к траектории. Единицей измерения количества движения является 1
, равная произведению массы точки на вектор ее скорости. Направлен этот вектор так же, как и скорость точки, т.е. по касательной к траектории. Единицей измерения количества движения является 1  · м/с = 1 Н·с.
· м/с = 1 Н·с.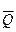 называется векторная сумма количеств движений всех точек системы:
называется векторная сумма количеств движений всех точек системы: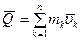 . (3.23)
. (3.23)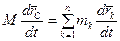 или
или 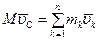 .
.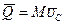 . (3.24)
. (3.24)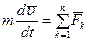 или, разделив переменные, можно записать
или, разделив переменные, можно записать . (3.25)
. (3.25)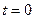 скорость
скорость  , а в момент
, а в момент 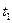 – скорость
– скорость  . Возьмем от выражения (3.25) определенные интегралы:
. Возьмем от выражения (3.25) определенные интегралы: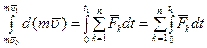 .
. называется элементарным импульсом силы
называется элементарным импульсом силы 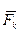 , а величина
, а величина 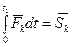 – импульсом силы
– импульсом силы  . (3.26)
. (3.26)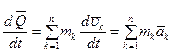 . Учитывая (3.11), получим теорему об изменении количества движения механической системы:
. Учитывая (3.11), получим теорему об изменении количества движения механической системы: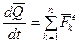 . (3.27)
. (3.27)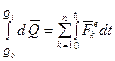 или
или  . (3.28)
. (3.28)


