Систему материальных точек или тел, движение которой рассматривается, называют механической системой. В статике действующие на механическую систему силы разделяют на активные  и реакции связей
и реакции связей 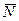 . В динамике чаще разделяют силы на внешние
. В динамике чаще разделяют силы на внешние 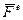 и внутренние
и внутренние  (индексы
(индексы 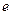 и
и  от латинских exterior – внешний и interior – внутренний). Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной механической системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга.
от латинских exterior – внешний и interior – внутренний). Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной механической системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга.
Отметим два свойства внутренних сил:
1. Главный вектор всех внутренних сил равняется нулю ( = 0).
= 0).
Выберем две произвольные точки  ,
,  механической системы и некоторый неподвижный центр О (рис.3.1). Силы взаимодействия этих точек обозначим через
механической системы и некоторый неподвижный центр О (рис.3.1). Силы взаимодействия этих точек обозначим через  и
и 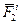 . Согласно аксиоме о равенстве действия и противодействия,
. Согласно аксиоме о равенстве действия и противодействия, 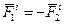 , или
, или 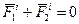 . Рассуждая аналогично, для всех точек системы, получим
. Рассуждая аналогично, для всех точек системы, получим
 (3.6)
(3.6)
2. Главный момент всех внутренних сил механической системы относительно произвольного центра равняется нулю ( ). Найдем сумму моментов сил
). Найдем сумму моментов сил  и
и 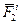 относительно центра О. По определению (1.4), с учетом того, что
относительно центра О. По определению (1.4), с учетом того, что 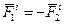 , получаем:
, получаем:
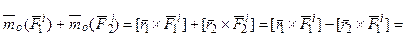

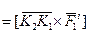 . Здесь
. Здесь  и
и 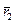 – радиус-векторы точек
– радиус-векторы точек  и
и  (рис. 3.1). Векторы
(рис. 3.1). Векторы  и
и  направлены по одной линии, поэтому их векторное произведение
направлены по одной линии, поэтому их векторное произведение 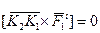 . Следовательно,
. Следовательно,  . Для всех точек системы
. Для всех точек системы
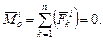
(3.7)
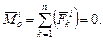 (3.7)
(3.7)
 и реакции связей
и реакции связей 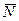 . В динамике чаще разделяют силы на внешние
. В динамике чаще разделяют силы на внешние 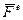 и внутренние
и внутренние  (индексы
(индексы 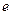 и
и  от латинских exterior – внешний и interior – внутренний). Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной механической системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга.
от латинских exterior – внешний и interior – внутренний). Внешними называют силы, действующие на точки системы со стороны точек или тел, не входящих в состав данной механической системы. Внутренними называют силы, с которыми точки или тела данной системы действуют друг на друга. = 0).
= 0). ,
,  механической системы и некоторый неподвижный центр О (рис.3.1). Силы взаимодействия этих точек обозначим через
механической системы и некоторый неподвижный центр О (рис.3.1). Силы взаимодействия этих точек обозначим через  и
и 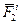 . Согласно аксиоме о равенстве действия и противодействия,
. Согласно аксиоме о равенстве действия и противодействия, 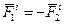 , или
, или 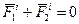 . Рассуждая аналогично, для всех точек системы, получим
. Рассуждая аналогично, для всех точек системы, получим (3.6)
(3.6) ). Найдем сумму моментов сил
). Найдем сумму моментов сил 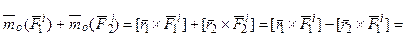

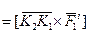 . Здесь
. Здесь  и
и 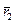 – радиус-векторы точек
– радиус-векторы точек  и
и 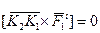 . Следовательно,
. Следовательно,  . Для всех точек системы
. Для всех точек системы



