Плоское движение твердого тела
Плоским (или плоскопараллельным) называется движение твердого тела, при котором все его точки перемещаются параллельно некоторой фиксированной неподвижной плоскости.
Плоское движение совершают многие части механизмов и машин, например катящееся колесо, произвольное движение книги по поверхности стола и т.д. Отметим, что при исследовании плоского движения книги достаточно определить движение одного ее листа. Пусть тело Уравнения
определяющие закон происходящего движения, называются уравнениями движения плоской фигуры в ее плоскости. Они же являются уравнениями плоскопараллельного движения твердого тела. Плоское движение можно рассматривать как составное движение, состоящее из поступательного движения фигуры с полюсом A и вращения фигуры вокруг этого полюса. Первые два уравнения в (2.29) определяют поступательное движение плоской фигуры с полюсом А, а третье уравнение – вращение фигуры вокруг полюса А. Можно доказать, что вращательная часть движения от выбора полюса не зависит.
а скорость точки В Таким образом, скорость произвольной точки тела при плоском движении геометрически складывается из скорости полюса в поступательном движении твердого тела и скорости, с которой эта точка вместе с телом вращается вокруг полюса.
Вектор 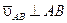 и численно равен и численно равен 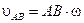 , где ω – угловая скорость плоской фигуры. Проектируя обе части равенства (2.30) на отрезок прямой АВ (рис.2.11), находим , где ω – угловая скорость плоской фигуры. Проектируя обе части равенства (2.30) на отрезок прямой АВ (рис.2.11), находим
Проекции скоростей двух точек тела на отрезок прямой, соединяющий эти точки, равны. При плоском движении в каждый момент времени существует точка
При качении колеса по неподвижной поверхности мгновенным центром скоростей является точка сцепления колеса с поверхностью (рис. 2.15). Если радиус колеса и скорость центра колеса известны, то можно определить мгновенную угловую скорость
|


 (рис. 2.8) движется параллельно плоскости
(рис. 2.8) движется параллельно плоскости 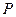 . В этом случае для исследования движения всего тела достаточно изучить, как движется в плоскости
. В этом случае для исследования движения всего тела достаточно изучить, как движется в плоскости 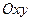 , параллельной плоскости
, параллельной плоскости 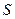 этого тела (рис. 2.9). Положение плоской фигуры S в сечении
этого тела (рис. 2.9). Положение плоской фигуры S в сечении 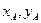 точки А и угол φ, который отрезок АВ образует с осью
точки А и угол φ, который отрезок АВ образует с осью 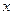 . Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом.
. Точку А, выбранную для определения положения фигуры S, будем в дальнейшем называть полюсом. ,
,  ,
, 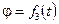 , (2.29)
, (2.29)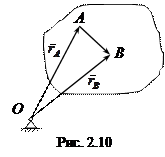 Пусть
Пусть  и
и  радиусы-векторы точек А и В плоской фигуры, причем
радиусы-векторы точек А и В плоской фигуры, причем 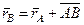 (рис. 2.10). Будем считать точку А полюсом. Отметим, что полюсом, как правило, считают точку, скорость и ускорение которой известны. По определению (2.2) скорость точки А
(рис. 2.10). Будем считать точку А полюсом. Отметим, что полюсом, как правило, считают точку, скорость и ускорение которой известны. По определению (2.2) скорость точки А ,
, . (2.30)
. (2.30)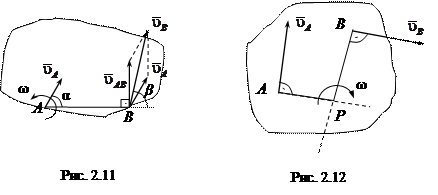
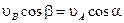 . (2.31)
. (2.31)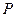 скорость которой равна нулю (
скорость которой равна нулю (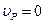 ). Такая точка называется мгновенным центром скоростей (МЦС). Движение плоской фигуры можно рассматривать как мгновенный поворот ее вокруг точки Р. Скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей:
). Такая точка называется мгновенным центром скоростей (МЦС). Движение плоской фигуры можно рассматривать как мгновенный поворот ее вокруг точки Р. Скорости точек плоской фигуры пропорциональны их расстояниям от мгновенного центра скоростей:  ;
; 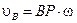 , где ω – угловая скорость плоской фигуры в данный момент времени. Чтобы
, где ω – угловая скорость плоской фигуры в данный момент времени. Чтобы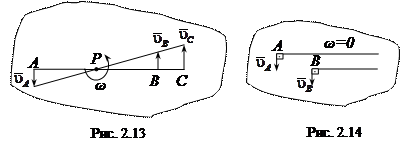
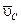 в сторону мгновенного поворота вокруг точки Р. Величина скорости будет
в сторону мгновенного поворота вокруг точки Р. Величина скорости будет 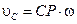 . Иллюстрация этого правила для случая, когда векторы скоростей разных точек плоской фигуры параллельны, показана на рис. 2.13.
. Иллюстрация этого правила для случая, когда векторы скоростей разных точек плоской фигуры параллельны, показана на рис. 2.13. Если перпендикуляры, восставленные к векторам
Если перпендикуляры, восставленные к векторам 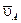 и
и 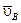 , не пересекаются, то скорости всех точек плоской фигуры в данный момент времени одинаковы (
, не пересекаются, то скорости всех точек плоской фигуры в данный момент времени одинаковы ( ), угловая скорость
), угловая скорость 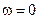 (рис.2.14). Такое состояние движения тела называют мгновенно поступательным.
(рис.2.14). Такое состояние движения тела называют мгновенно поступательным.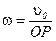 и скорости других точек:
и скорости других точек:  ;
; 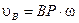 ,
, 


