Механической системы
Рассмотрим механическую систему, состоящую из Второй закон Ньютона для всех точек системы записывается в следующем виде:
В проекциях на оси координат это уравнение будет иметь вид
Теорема о движении центра масс. Дважды продифференцировав по времени уравнение (3.10), находим
Произведение массы системы на ускорение ее центра масс равно векторной сумме всех действующих на систему внешних сил. По внешнему виду это уравнение напоминает уравнение движения точки. Отличие состоит в том, что материальной точкой центр масс не является. Поэтому теорема о движении центра масс системы формулируется так: центр масс механической системы движется как материальная точка, к которой приложены действующие на систему все внешние силы, а масса точки равна массе всей системы. Из уравнения (3.13) следует, что движение центра масс возможно только при наличии внешних сил, внутренние же силы не могут изменить положения центра масс. Внутренние силы иногда являются причиной появления внешних сил. Например, внутренняя сила, приводящая в движение ведущее колесо автомобиля, вызывает действие на колесо внешней силы сцепления с дорогой, которая «толкает» автомобиль. Если дорогу принять за абсолютно гладкую плоскость, то сила сцепления равна нулю, и колесо будет двигаться таким образом, что его центр масс останется неподвижным (явление пробуксовки). Отметим, что уравнение (3.13) является также дифференциальным уравнением поступательного движения твердого тела. Действительно, при поступательном движении ускорения всех точек в каждый момент времени одинаковы и, следовательно, равны ускорению центра масс тела, которое определяется теоремой о движении центра масс. Рассмотрим частные случаи. а) Пусть сумма внешних сил, действующих на систему, равна нулю: б) Если при отсутствии внешних сил в начальный момент времени центр масс был в покое, то он и останется в покое:
|

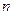 материальных точек. Выберем произвольную точку
материальных точек. Выберем произвольную точку  системы. На нее действуют внешние и внутренние силы. Равнодействующие этих сил
системы. На нее действуют внешние и внутренние силы. Равнодействующие этих сил 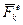 и
и 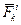 (рис. 3.2).
(рис. 3.2).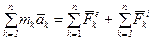 . Учитывая свойство внутренних сил (3.6), получим дифференциальное уравнение движения механической системы в векторной форме:
. Учитывая свойство внутренних сил (3.6), получим дифференциальное уравнение движения механической системы в векторной форме: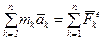 или
или 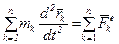 . (3.11)
. (3.11)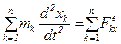 ,
,  ,
, 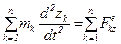 . (3.12)
. (3.12)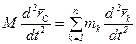 или
или 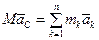 . Учитывая (3.11), получим
. Учитывая (3.11), получим . (3.13)
. (3.13)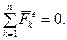 Тогда из уравнения (3.13) следует, что
Тогда из уравнения (3.13) следует, что  и
и 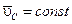 . Следовательно,при отсутствии внешних сил центр масс системы движется прямолинейно и равномерно.
. Следовательно,при отсутствии внешних сил центр масс системы движется прямолинейно и равномерно. ,
, 
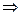
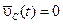 .
.


