Теорема об изменении момента количества движения системы
Здесь выражение в квадратных скобках − векторное произведение радиус-вектора Вычислим от равенства (3.29) производную по времени:
В полученном выражении
Доказана теорема моментов относительно центра: производная по времени от момента количества движения точки, взятого относительно какого-нибудь неподвижного центра, равна моменту действующей на точку силы относительно того же центра. Определим момент количества движения (кинетический момент) твердого тела, вращающегося вокруг неподвижной оси
Кинетический момент твердого тела относительно оси вращения равен произведению момента инерции тела относительно данной оси на угловую скорость тела. Докажем теорему моментов для механической системы. Выражение (3.30) для
где
Последняя сумма по свойству внутренних сил равна нулю. Учитывая, что кинетический момент системы относительно центра
Производная по времени от кинетического момента механической системы относительно неподвижного центра равна сумме моментов внешних сил относительно того же центра. Проектируя обе части (3.32) на ось
Для вращающегося твердого тела выполняется равенство (3.31), поэтому выражение (3.33) можно представить в другом виде:
Уравнение (3.34) называется дифференциальным уравнением вращательного движения твердого тела. Произведение момента инерции твердого тела относительно оси
|

 Моментом количества движения точки
Моментом количества движения точки  относительно некоторого центра
относительно некоторого центра 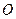 называется векторная величина
называется векторная величина  , определяемая равенством
, определяемая равенством . (3.29)
. (3.29)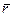 на вектор количества движения
на вектор количества движения  движущейся точки
движущейся точки 

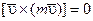 , как векторное произведение двух параллельных векторов. Согласно (1.4) справедливо равенство
, как векторное произведение двух параллельных векторов. Согласно (1.4) справедливо равенство  . В результате, получается
. В результате, получается . (3.30)
. (3.30)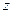 с угловой скоростью
с угловой скоростью 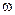 . Считаем, что тело состоит из
. Считаем, что тело состоит из 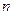 материальных точек. Выберем произвольную точку K, отстоящей от оси
материальных точек. Выберем произвольную точку K, отстоящей от оси  . Момент количества движения точки K относительно оси
. Момент количества движения точки K относительно оси  . Кинетический момент вращающегося тела относительно оси
. Кинетический момент вращающегося тела относительно оси 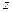 :
: 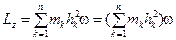 . Величина, стоящая в скобках, представляет собой момент инерции тела относительно оси
. Величина, стоящая в скобках, представляет собой момент инерции тела относительно оси 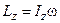 . (3.31)
. (3.31)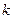 – ой точки системы можно записать так:
– ой точки системы можно записать так:
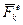 и
и 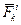 – равнодействующие всех внешних и внутренних сил, действующих на точку. Для механической системы
– равнодействующие всех внешних и внутренних сил, действующих на точку. Для механической системы
 , получим
, получим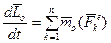 . (3.32)
. (3.32)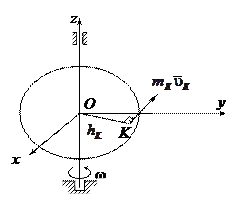
 . (3.33)
. (3.33) или
или . (3.34)
. (3.34) ) тела, вращающегося вокруг оси
) тела, вращающегося вокруг оси 


