Моменты инерции
Движение механической системы зависит не только от массы тела, но и от момента инерции. Момент инерции есть мера инертности при вращательном движении тела. Осевой момент инерции относительно оси
Из определения следует, что осевой момент инерции тела или системы относительно любой оси является величиной положительной. По теореме Пифагора
Аналогично вычисляются моменты инерции относительно других осей:
Найдем осевые моменты инерции некоторых однородных тел. Тонкий однородный стержень длиной
Для вычисления момента инерции стержня относительно центральной оси нужно в (3.16) изменить пределы интегрирования. В этом случае
Выделим элементарное сечение в виде кольца радиуса
Используя (3.18), можно вычислить а) Момент инерции тонкостенного цилиндра или кольца радиуса
б) Момент инерции сплошного цилиндра или круглой пластины радиуса
Радиусом инерции тела относительно оси z называется линейная величина
 . (3.21) . (3.21)
Найдем зависимость между моментами инерции относительно параллельных осей. Пусть ось
Координаты точки
Из второй формулы (3.9) следует
Формула (3.22) выражает теорему Гюйгенса-Штейнера: момент инерции тела относительно какой-либо оси равен моменту инерции этого тела относительно параллельной оси, проходящей через центр масс, плюс произведение массы тела на квадрат расстояния между этими осями.
|

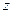 равен сумме произведений массы
равен сумме произведений массы  каждой точки системы на квадрат ее расстояния до оси (рис. 3.3):
каждой точки системы на квадрат ее расстояния до оси (рис. 3.3):
 . (3.14)
. (3.14) , следовательно
, следовательно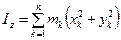 .
. ,
,  . (3.15)
. (3.15) и массой
и массой 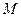 . Сначала вычислим момент инерции относительно оси
. Сначала вычислим момент инерции относительно оси 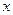 от оси
от оси  и массой
и массой  ·
·  . Момент инерции элемента
. Момент инерции элемента  ·
·  . (3.16)
. (3.16) . (3.17)
. (3.17) Цилиндр. Вычислим момент инерции полого цилиндра массой M относительно продольной оси z. Цилиндр радиуса R имеет отверстие радиуса r (рис. 3.5). Ось цилиндра перпендикулярна к рисунку.
Цилиндр. Вычислим момент инерции полого цилиндра массой M относительно продольной оси z. Цилиндр радиуса R имеет отверстие радиуса r (рис. 3.5). Ось цилиндра перпендикулярна к рисунку.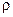 и толщиной
и толщиной 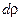 . Учитывая, что масса единицы площади сечения равна
. Учитывая, что масса единицы площади сечения равна  , получаем массу элементарного цилиндра радиуса
, получаем массу элементарного цилиндра радиуса  . Здесь
. Здесь  – площадь элементарного сечения,
– площадь элементарного сечения, 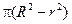 - площадь сечения полого цилиндра. Момент инерции полого цилиндра
- площадь сечения полого цилиндра. Момент инерции полого цилиндра . (3.18)
. (3.18) в частных случаях:
в частных случаях: . Полагая в формуле (3.18)
. Полагая в формуле (3.18)  , получаем
, получаем . (3.19)
. (3.19) , находим:
, находим: . (3.20)
. (3.20) , определяемая равенством
, определяемая равенством
 проходит через центр масс
проходит через центр масс 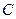 тела, а ось
тела, а ось 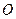 на расстоянии
на расстоянии  от оси
от оси  , (а)
, (а)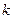 в системах
в системах  и
и  связаны соотношениями
связаны соотношениями 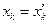 ;
;  . Подставляя эти координаты в выражение (б), получим:
. Подставляя эти координаты в выражение (б), получим: 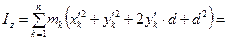

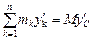 . Так как ось
. Так как ось  , следовательно,
, следовательно,  . Кроме того
. Кроме того  . Учитывая полученные равенства и выражение для
. Учитывая полученные равенства и выражение для 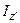 , находим
, находим . (3.22)
. (3.22)


