Кинетической энергией материальной точки k называется скалярная величина, равная половине произведения массы точки на квадрат ее скорости  . Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы
. Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы
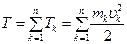 . (3.35)
. (3.35)
Найдем формулы для вычисления кинетической энергии тел в разных случаях движения.
Поступательное движение. В этом случае скорости всех точек тела одинаковы  , где
, где  скорость центра масс тела.
скорость центра масс тела.
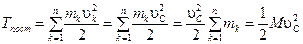 . (3.36)
. (3.36)
Вращательное движение. Скорость 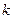 –ой точки тела
–ой точки тела 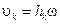 , где
, где 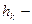 расстояние точки до оси вращения.
расстояние точки до оси вращения.
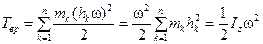 , (3.37)
, (3.37)
где  момент инерции тела относительно оси вращения
момент инерции тела относительно оси вращения 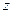 .
.
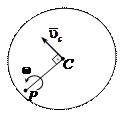
Плоское движение. Из кинематики известно, что плоское движение в некоторый момент времени можно рассматривать как мгновенный поворот тела вокруг оси, проходящей через мгновенный центр скоростей.
В этом случае 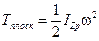 . Пусть точка
. Пусть точка 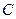 – центр масс. По теореме Гюйгенса-Штейнера (3.22):
– центр масс. По теореме Гюйгенса-Штейнера (3.22): 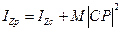 . Кинетическая энергия тела при плоском движении
. Кинетическая энергия тела при плоском движении

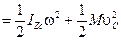 . (3.38)
. (3.38)
Здесь  момент инерции тела относительно центральной оси,
момент инерции тела относительно центральной оси,  скорость центра масс,
скорость центра масс,  мгновенная угловая скорость,
мгновенная угловая скорость, 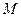 – масса тела.
– масса тела.
Докажем теорему об изменении кинетической энергии для материальной точки. Запишем второй закон Ньютона в проекции на касательную (3.5):  . Касательное ускорение
. Касательное ускорение 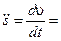
 . Следовательно, закон Ньютона примет вид
. Следовательно, закон Ньютона примет вид
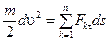 или
или 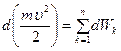 , (3.39)
, (3.39)
где 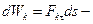 элементарная работа силы
элементарная работа силы 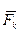 на перемещении
на перемещении 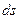 точки
точки 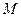 . Элементарную работу можно записать иначе:
. Элементарную работу можно записать иначе:

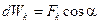
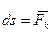 ·
· 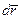 . (3.40)
. (3.40)
Здесь 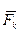 ·
· 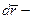 скалярное произведение векторов,
скалярное произведение векторов, 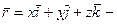 радиус-вектор точки
радиус-вектор точки 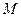 .
.
Поскольку 
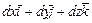 , то аналитическое выражение элементарной работы силы
, то аналитическое выражение элементарной работы силы 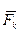 :
:
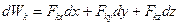 . (3.41)
. (3.41)
Проинтегрировав (3.39) в пределах изменения переменных в точках 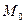 и
и  , найдем окончательно
, найдем окончательно
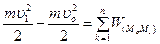 . (3.42)
. (3.42)
Это уравнение выражает теорему об изменении кинетической энергии материальной точки в интегральной форме: изменение кинетической энергии точки на некотором ее перемещении равно сумме работ приложенных сил на том же перемещении.
Для произвольной точки 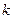 механической системы выражение(3.42) имеет вид:
механической системы выражение(3.42) имеет вид: 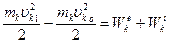 . Для всей системы
. Для всей системы 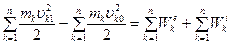 . Если обозначить кинетическую энергию всей системы в ее начальном положении
. Если обозначить кинетическую энергию всей системы в ее начальном положении
 , а в конечном положении
, а в конечном положении  , то
, то
 . (3.43)
. (3.43)
Уравнение (3.43) выражает теорему об изменении кинетической энергии механической системы в интегральной форме: изменение кинетической энергии системы при некотором ее перемещении равно сумме работ на этом перемещении всех приложенных к системе внешних и внутренних сил. Отметим, что в общем случае сумма работ внутренних сил не равна нулю. Для абсолютно твердого тела 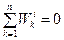 , так как расстояния между любыми точками тела не изменяются.
, так как расстояния между любыми точками тела не изменяются.
Работа силы тяжести. Пусть точка 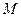 переместилась под действием силы тяжести
переместилась под действием силы тяжести  из положения
из положения 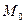 в положение
в положение  (рис. 3.7). По формуле (3.41) найдем элементарную работу силы
(рис. 3.7). По формуле (3.41) найдем элементарную работу силы  :
: 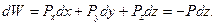 Полная работа силы
Полная работа силы  на перемещении
на перемещении  будет
будет 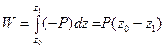 или
или
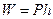 , (3.44)
, (3.44)
где
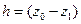
− высота, на которую опустилась точка. Таким образом, работа силы тяжести положительна, когда точка опускается, и отрицательна, когда точка поднимается.
Работа силы упругости пружины. Пусть груз 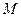 прикреплен к пружине жесткости с (рис. 3.8). Выберем начало координаты
прикреплен к пружине жесткости с (рис. 3.8). Выберем начало координаты 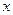 в положении
в положении 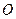 , при котором пружина не деформирована (ее длина равна l
, при котором пружина не деформирована (ее длина равна l 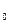 ), и определим работу силы упругости
), и определим работу силы упругости 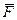 пружины при перемещении ее нижнего конца из начального положения
пружины при перемещении ее нижнего конца из начального положения 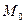 в конечное положение
в конечное положение  . Пусть λ
. Пусть λ 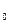 , λ
, λ 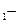 начальная и конечная деформации пружины. Согласно закону Гука
начальная и конечная деформации пружины. Согласно закону Гука  . Проекции силы
. Проекции силы 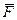 на оси координат:
на оси координат: 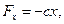
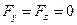 . Элементарная работа
. Элементарная работа 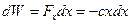 . Полная работа
. Полная работа
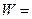
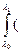 –
– 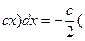 λ
λ 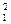 –λ
–λ 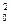 )или
)или 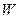 =
= 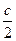 (λ
(λ 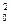 –λ
–λ 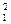 ). (3.45)
). (3.45)
Работа силы упругости положительна, если начальная λ 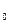 деформация пружины больше конечной λ
деформация пружины больше конечной λ 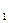 .
.
Работа силы трения скольжения. Пусть тело 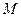 перемещается по наклонной шероховатой плоскости из положения
перемещается по наклонной шероховатой плоскости из положения 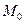 в положение
в положение  . Действующая на тело сила трения
. Действующая на тело сила трения  , где
, где 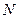 – нормальная реакция плоскости,
– нормальная реакция плоскости,  – коэффициент трения скольжения. Сила трения направлена противоположно перемещению тела, поэтому работа силы трения отрицательна. Если считать силу трения во время движения постоянной, то
– коэффициент трения скольжения. Сила трения направлена противоположно перемещению тела, поэтому работа силы трения отрицательна. Если считать силу трения во время движения постоянной, то
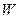
=
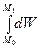
=
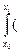
–
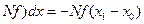
. (3.46)
В данном случае 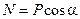 ,
,  , следовательно
, следовательно
 .
.
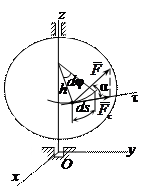
Работа силы, приложенной к вращающемуся телу. Для тела, вращающегося вокруг оси 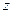 , элементарная работа приложенной к телу силы
, элементарная работа приложенной к телу силы 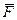 равна
равна 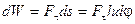 , где
, где 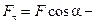 модуль касательной составляющей силы
модуль касательной составляющей силы 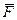 ,
,  – элементарный угол поворота тела вокруг оси
– элементарный угол поворота тела вокруг оси 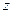 . Нетрудно заметить, что
. Нетрудно заметить, что  – момент силы
– момент силы 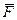 относительно оси вращения
относительно оси вращения 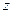 . Будем называть величину
. Будем называть величину 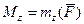 вращающим моментом. Тогда элементарная работа
вращающим моментом. Тогда элементарная работа 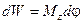 . При повороте на конечный угол
. При повороте на конечный угол  работа
работа
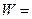
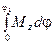 , (3.47)
, (3.47)
а в случае постоянного момента из (3.47) следует 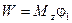 .
.
Вопросы для самоконтроля
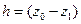 − высота, на которую опустилась точка. Таким образом, работа силы тяжести положительна, когда точка опускается, и отрицательна, когда точка поднимается.
− высота, на которую опустилась точка. Таким образом, работа силы тяжести положительна, когда точка опускается, и отрицательна, когда точка поднимается.
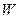 =
= 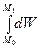 =
= 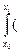 –
– 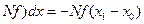 . (3.46)
. (3.46)

 . Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы
. Кинетической энергией механической системы называется арифметическая сумма кинетических энергий всех точек системы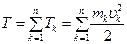 . (3.35)
. (3.35) , где
, где  скорость центра масс тела.
скорость центра масс тела.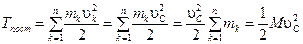 . (3.36)
. (3.36)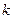 –ой точки тела
–ой точки тела 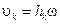 , где
, где 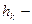 расстояние точки до оси вращения.
расстояние точки до оси вращения.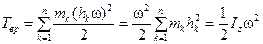 , (3.37)
, (3.37) момент инерции тела относительно оси вращения
момент инерции тела относительно оси вращения 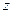 .
.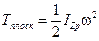 . Пусть точка
. Пусть точка 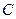 – центр масс. По теореме Гюйгенса-Штейнера (3.22):
– центр масс. По теореме Гюйгенса-Штейнера (3.22): 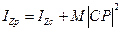 . Кинетическая энергия тела при плоском движении
. Кинетическая энергия тела при плоском движении

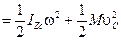 . (3.38)
. (3.38) момент инерции тела относительно центральной оси,
момент инерции тела относительно центральной оси,  мгновенная угловая скорость,
мгновенная угловая скорость, 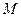 – масса тела.
– масса тела. . Касательное ускорение
. Касательное ускорение 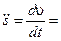
 . Следовательно, закон Ньютона примет вид
. Следовательно, закон Ньютона примет вид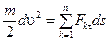 или
или 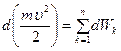 , (3.39)
, (3.39)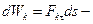 элементарная работа силы
элементарная работа силы 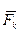 на перемещении
на перемещении 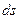 точки
точки 
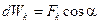
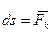 ·
· 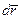 . (3.40)
. (3.40)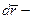 скалярное произведение векторов,
скалярное произведение векторов, 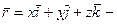 радиус-вектор точки
радиус-вектор точки 
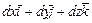 , то аналитическое выражение элементарной работы силы
, то аналитическое выражение элементарной работы силы 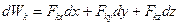 . (3.41)
. (3.41)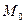 и
и  , найдем окончательно
, найдем окончательно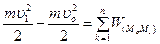 . (3.42)
. (3.42)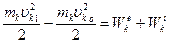 . Для всей системы
. Для всей системы 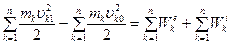 . Если обозначить кинетическую энергию всей системы в ее начальном положении
. Если обозначить кинетическую энергию всей системы в ее начальном положении , а в конечном положении
, а в конечном положении  , то
, то . (3.43)
. (3.43)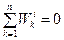 , так как расстояния между любыми точками тела не изменяются.
, так как расстояния между любыми точками тела не изменяются. из положения
из положения 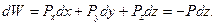 Полная работа силы
Полная работа силы  будет
будет 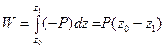 или
или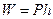 , (3.44)
, (3.44)
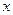 в положении
в положении 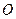 , при котором пружина не деформирована (ее длина равна l
, при котором пружина не деформирована (ее длина равна l 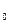 ), и определим работу силы упругости
), и определим работу силы упругости 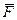 пружины при перемещении ее нижнего конца из начального положения
пружины при перемещении ее нижнего конца из начального положения 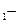 начальная и конечная деформации пружины. Согласно закону Гука
начальная и конечная деформации пружины. Согласно закону Гука  . Проекции силы
. Проекции силы 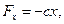
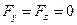 . Элементарная работа
. Элементарная работа 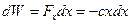 . Полная работа
. Полная работа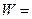
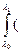 –
– 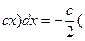 λ
λ 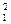 –λ
–λ 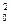 )или
)или 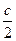 (λ
(λ 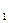 .
.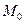 в положение
в положение  , где
, где 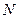 – нормальная реакция плоскости,
– нормальная реакция плоскости,  – коэффициент трения скольжения. Сила трения направлена противоположно перемещению тела, поэтому работа силы трения отрицательна. Если считать силу трения во время движения постоянной, то
– коэффициент трения скольжения. Сила трения направлена противоположно перемещению тела, поэтому работа силы трения отрицательна. Если считать силу трения во время движения постоянной, то
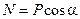 ,
,  , следовательно
, следовательно .
.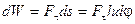 , где
, где 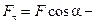 модуль касательной составляющей силы
модуль касательной составляющей силы  – элементарный угол поворота тела вокруг оси
– элементарный угол поворота тела вокруг оси  – момент силы
– момент силы 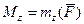 вращающим моментом. Тогда элементарная работа
вращающим моментом. Тогда элементарная работа 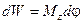 . При повороте на конечный угол
. При повороте на конечный угол  работа
работа
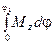 , (3.47)
, (3.47)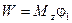 .
.


