Задача С-4 – на равновесие тела под действием произвольной пространственной системы сил. При ее решении нужно учесть, что реакции сферического шарнира и подпятника имеют три составляющие (по всем трем координатным осям), реакция цилиндрического шарнира (подшипника) – две составляющие, направленные по осям, перпендикулярным оси шарнира (подшипника). Шесть неизвестных реакций связей нужно определить из шести уравнений равновесия:
 ;
;  ;
;  ;
;
 ;
;  ;
;  .
.

Последние три уравнения – это моменты сил относительно осей координат. Моменты сил рекомендуется определять, применяя теорему Вариньона, по формулам (1.7), (1.8).

Тема 2: «Кинематика точки»
Задача К- 1
Тема этой задачи – координатный способ задания движения точки.
Постановка задачи. По заданному закону движения точки  ,
,  найти уравнение траектории; для момента времени
найти уравнение траектории; для момента времени 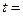 1с определить: положение точки на траектории, проекции скорости на координатные оси и её модуль, проекции ускорения на координатные и естественные оси и модуль ускорения, радиус кривизны траектории. Особое внимание уделить рисунку, на котором необходимо изобразить траекторию, векторы скорости, ускорения и их составляющие.
1с определить: положение точки на траектории, проекции скорости на координатные оси и её модуль, проекции ускорения на координатные и естественные оси и модуль ускорения, радиус кривизны траектории. Особое внимание уделить рисунку, на котором необходимо изобразить траекторию, векторы скорости, ускорения и их составляющие.
Уравнения движения выбираются по шифру из Таблицы К-1.
Таблица К-1
|
шифр
|  (см)
(см)
|  (см)
(см)
|
шифр
|  (см)
(см)
|  (см)
(см)
|
|
| 3–2t²
| –5t
|
| 3cos(πt²)
| 3sin(πt²)
|
|
| 3–cos(πt²/3)   
| –1+sin(πt²/3)
|
| –3–2sin(πt²/3)
| –cos(πt²/3)+5
|
|
| –7cos²(πt/6)
| 7sin²(πt/6)+5
|
| 2sin(πt²/6)–1
| 3cos(πt²/6)+1
|
|
| 7sin(πt²/6)–5
| 7cos(πt²/6)+1
|
| 5t²+5t/3–3
| 3t²+t+3
|
|
| 8t
| 4t²+1
|
| –2/(t+1)
| –2–2t
|
|
| 5–9cos²(πt²/6)
| 3–9sin²(πt²/6)
|
| 2–3cos(πt/3)
| 2sin(πt/3)–1
|
|
| –2–2t
| –2/(t+1)
|
| 4–2cos(πt/2)
| 4sin(πt/2)–1
|
|
| –2–2t²
| –6t
|
| 8sin(πt)
| 8cos(πt)
|
|
| 5sin²(πt²/6)
| 5cos²(πt²/6)
|
| 4cos(4πt)
| 2sin²(2πt)
|
|
| 4–5t²+5t/3
| 3–3t²+t
|
| 2t
| t–3t²
|
|
| –4cos(πt/3)
| –2sin(πt/3)–3
|
| 2–3t–6t²
| 3–3t/2–3t²
|
|
| 5t
| 7t²–3
|
| 4cos(πt/3)
| –3sin(πt/3)
|
|
| 7sin(πt²/6)
| 2–7cos(πt²/6)
|
| 5t²–3
| 8t
|
|
| 3sin(πt²/3)+3
| 3cos(πt²/3)+1
|
| 3sin²(πt²/6)
| 6cos²(πt²/6)
|
|
| 4cos²(πt/3)+2
| 4sin²(πt/3)–1
|
| –5+2t²
| 4–3t
|
|
| 4cos(πt/3)
| –3sin(πt/3)
|
| 3–9sin(πt²/6)
| 5–9cos(πt²/6)
|
Окончание таблицы К-1
|
| –8sin²(πt²/6)
| 8cos²(πt²/6)+2
|
| 3cos(2πt)
| 3sinπt
|
|
| –4/(t+1)
| 4t+4
|
| –4 (t+1)
| 4 (t+1)
|
|
| sin(πt²/3)–1
| –cos(πt²/3)+3
|
| –2sin(πt²/3)
| –4cos(πt²/3)
|
|
| 10cos(2πt/5)
| 10sin(2πt/5)
|
| 4 +2t–6t²
| 3+t–3t²
|
|
| –3cos(πt/3)+4
| 2sin(πt/3)
|
| –2cos(πt)
| 4sin²(πt)–1
|
|
| –3cos(πt²/6)
| 3sin(πt²/6)+1
|
| 1+3cos²(πt²/6)+
| 3+3sin²(πt²/6)
|
|
| 5t²–5t/3–2
| 3t²–t+1
|
| t²+2t+1
| 1/(t+1)
|
|
| 3cos(πt/4)
| 2sin(πt/4)
|
| 3t²–5
| 7t
|
|
| –2t–2
| –2/(t+1)
|
| 3cos²(πt²)
| 4sin²(πt²)
|
|
| t²
| 3t
|
| 2cos(πt²/6)
| 3sin(πt²/6)
|
|
| 3t
| –5t²–4
|
| 4t²+2
| 1/(2t²+1)
|
|
| –3/(t+2)
| 3t+6
|
| 3–6sin(πt/6)
| 4–9cos(πt/6)
|
|
| 3–3t/2–3t²
| 2–3t–6t²
|
| 3sin(πt/6)
| –6cos²(πt/6)
|
|
| 3t²+2
| –4t
|
| 2t+4
| t²
|
|
| 5t
| 3t²+1
|
| 8t+1
| 2t²–1
|
|
| –4t²+1
| –3t
|
| 4sin²(πt²/3)
| 4cos²(πt²/3)
|
|
| 5cos(πt²/3)
| –5sin(πt²/3)
|
| –4t
| 3t²+2
|
|
| 2cos(2πt)
| 2cos(πt)
|
| 10cos(πt/3)
| 10sin(πt/3)
|
|
| –5t
| 2t²+3
|
| 2cos(πt/2)
| 4sin²(πt/2)
|
|
| 4t
| t²
|
| sin(πt²/3)–1
| cos(πt²/3)+1
|
|
| 2cos(πt/6)+1
| 2sin(πt/6)–2
|
| 2t
| t²+3
|
|
| 3t+6
| –3/(t+2)
|
| 12sin(4πt)
| 12sin(2πt)
|
|
| 4sin(πt/2)
| 3sin(πt/2)
|
| 6sin(πt²)
| 6cos(πt²)
|
|
| 2–7cos(πt²/6)
| 3+7sin(πt²/6)
|
| 2t²+1
| 8t
|
|
| 8–6sin(2πt)
| 5–8cos(2πt)
|
| 2–3cos(πt²/3)
| 2sin(πt²/3)
|
|
| 2(1–sin(πt))
| 2(2–cos(πt))
|
| –8t
| 2t²+6
|
|
| 5cos²(πt/6)
| –5cos²(πt/6)
|
| 3t+6
| –3/(t+2)
|
|
| –3t²–4
| 5t
|
| 8cos²(πt²/6)
| 8sin²(πt²/6)
|
|
| 5cos(πt²/3)
| –5sin(πt²/3)
|
| 4sin(πt/6)
| 6cos(πt/6)
|
|
| 6sin(πt²/6)–2
| 6cos(πt²/6)+3
|
| 4–2t
| t²–2
|
|
| 4t²+1
| 6t
|
| 10sin(πt²/6)
| 4–8cos(πt²/6)
|
|
| 3–3t²+t
| 4–5t²+5t/3
|
| 4–2t
| (t+1)²
|
|
| 3sin(πt/3)
| 2sin(πt/3)
|
| 2t+2
| 2(t+1)²
|
|
| –6t
| –2t²–4
|
| 2t
| t²+1
|
Тема 3: «Кинематика твeрдого тела»

 ;
;  ;
;  ;
; ;
;  ;
;  .
.

 ,
,  найти уравнение траектории; для момента времени
найти уравнение траектории; для момента времени 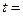 1с определить: положение точки на траектории, проекции скорости на координатные оси и её модуль, проекции ускорения на координатные и естественные оси и модуль ускорения, радиус кривизны траектории. Особое внимание уделить рисунку, на котором необходимо изобразить траекторию, векторы скорости, ускорения и их составляющие.
1с определить: положение точки на траектории, проекции скорости на координатные оси и её модуль, проекции ускорения на координатные и естественные оси и модуль ускорения, радиус кривизны траектории. Особое внимание уделить рисунку, на котором необходимо изобразить траекторию, векторы скорости, ускорения и их составляющие.




