Поступательное и вращательное движения твердого тела
В кинематике, как и в статике, будем считать все твердые тела как абсолютно твердые. Задачи кинематики твердого тела разделяются на две части: 1) задание движения и определение кинематических характеристик движения тела в целом; 2) определение кинематических характеристик движения отдельных точек тела. Решая задачу кинематики твердого тела, нужно, прежде всего, установить вид движения. Различают пять видов движения твердого тела: 1) поступательное движение твердого тела; 2) вращение твердого тела вокруг неподвижной оси; 3) плоское (плоскопараллельное) движение твердого тела; 4) движение твердого тела с одной неподвижной точкой; 5) сложное движение твердого тела. Начнем с рассмотрения поступательного движения твердого тела. Поступательным движением твердого тела называется такое движение, при котором любая прямая, соединяющая две точки тела, движется параллельно самой себе. Все точки твердого тела, движущегося поступательно, описывают одинаковые траектории и в каждый момент времени имеют геометрически равные скорости и ускорения. Поступательное движение не следует смешивать с прямолинейным движением. При поступательном движении тела траектории его точек могут быть любыми кривыми линиями. ` Приведем примеры. 1. Кузов автомобиля на прямом горизонтальном участке дороги движется поступательно. Траектории всех точек кузова будут прямыми линиями. 2. Педаль велосипеда относительно рамы движется поступательно, а все точки педали движутся по окружностям. Поступательное движение твердого тела вполне определяется движением какой-нибудь одной его точки. Следовательно, изучение поступательного движения тела сводится к уже рассмотренной задаче кинематики точки. Вращательным называется такое движение твердого тела, при котором какие-нибудь две точки, принадлежащие телу (или неизменно с ним связанные) остаются во все время движения неподвижными. Проходящая через неподвижные точки прямая, называется осью вращения. Выберем неподвижную плоскость N, принимаемую за начало отсчета, а также жестко связанную с телом плоскость Р, которая вращается вместе с ним вокруг оси Оz (рис. 2.6). Угол между введенными плоскостями φ называется углом поворота (измеряется в радианах). Угол φ считается положительным, если при взгляде с положительного направления оси вращения он отсчитывается против хода часовой стрелки.
Положение вращающегося тела в каждый момент времени будет известно, если задана зависимость угла поворота от времени:
Это уравнение выражает закон вращательного движения твердого тела вокруг неподвижной оси. Производная по времени от угла поворота называется алгебраической угловой скоростью:
Угловая скорость показывает как быстро и в каком направлении вращается тело. Единицей измерения угловой скорости является рад/с или сокращенно – с-1. При равномерном вращении угловая скорость постоянна: В технике часто скорость вращения тела задают частотой вращения Производная по времени от алгебраической угловой скорости называется угловым ускорением:
Единицей измерения углового ускорения является рад/c–2 или сокращенно – c–2. Если в некоторый момент времени Вращение с постоянным угловым ускорением (
где Так как
Определим скорость и ускорение точек вращающегося тела. Пусть тело ОА (рис. 2.7) вращается вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку О согласно закону (2.21). Все точки вращающегося тела, не находящиеся на оси вращения, движутся по окружностям. Например, траекторией точки А является окружность радиуса
Вектор скорости С учетом (2.26) и (2.23) найдем по формулам (2.15) и (2.16) касательное и нормальное ускорения точки А:
Модуль ускорения точки А равен
Итак, зная закон вращения тела (2.21) и расстояние точки тела до оси вращения, можно по формулам (2.26) – (2.28) определить скорость и ускорение любой точки вращающегося тела.
|


 . (2.21)
. (2.21) или
или  . (2.22)
. (2.22) .
. , т.е. числом оборотов, совершаемых телом за одну минуту. Найдем зависимость между
, т.е. числом оборотов, совершаемых телом за одну минуту. Найдем зависимость между  с-1. При одном обороте тело повернется на угол 2π, а при
с-1. При одном обороте тело повернется на угол 2π, а при  ; этот поворот совершается за время
; этот поворот совершается за время  1 мин = 60 с. Тогда
1 мин = 60 с. Тогда  с-1.
с-1. или
или  . (2.23)
. (2.23) и
и  или
или 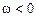 и
и  , то в данный момент вращение тела называется ускоренным. Если знаки
, то в данный момент вращение тела называется ускоренным. Если знаки  разные, то вращение тела называется замедленным.
разные, то вращение тела называется замедленным. ) называется равнопеременным. Разделяя переменные равенства (2.23), получим
) называется равнопеременным. Разделяя переменные равенства (2.23), получим  . Проинтегрируем левую часть этого равенства от
. Проинтегрируем левую часть этого равенства от  до
до  , а правую – от
, а правую – от  до
до  :
:  Следовательно,
Следовательно, (2.24)
(2.24) – начальная угловая скорость.
– начальная угловая скорость.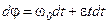 . Интегрируем последнее выражение при изменении угла поворота от φ0 до φ и времени от 0 до t:
. Интегрируем последнее выражение при изменении угла поворота от φ0 до φ и времени от 0 до t:  . Вычисляя интегралы, получим закон равнопеременного вращения:
. Вычисляя интегралы, получим закон равнопеременного вращения: . (2.25)
. (2.25) . При повороте тела на угол φ точка А перемещается по дуге окружности на
. При повороте тела на угол φ точка А перемещается по дуге окружности на  . Скорость точки А определяется по формуле (2.12):
. Скорость точки А определяется по формуле (2.12): или
или  . (2.26)
. (2.26)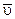 направлен по касательной к окружности в направлении поворота тела. Таким образом, числовое значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.
направлен по касательной к окружности в направлении поворота тела. Таким образом, числовое значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние от этой точки до оси вращения.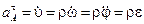 ,
,  . (2.27)
. (2.27)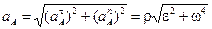 . (2.28)
. (2.28)


