Кинематика точки
В кинематике изучаются геометрические законы механического движения материальных тел без учета их масс и причин, вызывающих это движение. Изучение кинематики начинают с изучения движения точки (кинематика точки). Основная задача кинематики точки состоит в том, чтобы по заданному закону движения точки найти ее основные кинематические характеристики: траекторию, скорость и ускорение. Непрерывная линия, которую описывает движущаяся точка, называется траекторией точки. Если траекторией является прямая линия, движение точки называется прямолинейным, а если кривая – криволинейным. Движение тел совершается в пространстве с течением времени. За единицу длины при изменении расстояний принимается 1м. За единицу времени принята 1с. В задачах кинематики время t принимают за независимое переменное (аргумент). Все другие переменные (расстояния, скорости, ускорения) рассматриваются как изменяющиеся с течением времени, т.е. как функции времени t. Основы, на которых строится кинематика, дают аксиомы геометрии. Никаких дополнительных законов или аксиом для изучения движения тел не требуется. В зависимости от выбора системы отсчета существует три способа задания движения точки: векторный, координатный и естественный. Векторный способ задания движения точки. Положение точки в пространстве однозначно определяется заданием радиус-вектора
Траектория точки является геометрическим местом концов радиус-вектора Пусть в момент времени t точка занимает положение М, определяемое радиус-вектором
Таким образом, вектор скорости точки в данный момент равен производной от радиус-вектора точки по времени. Вектор При неравномерном криволинейном движении точки изменяются модуль и направление ее скорости. Величина, характеризующая изменение скорости точки, называется ускорением точки. Ускорение, так же как и скорость, величина векторная. Если за промежуток времени
Следовательно, вектор ускорения точки равен первой производной от скорости или второй производной от радиус-вектора точки по времени. Координатный способ задания движения точки. Положение точки М в системе отсчета Оxyz определяется тремя координатами точки х, у, z. Так как радиус-вектор точки М можно выразить через координаты
то вместо движения точки в векторной форме (2.1) можно представить параметрические уравнения движения точки в координатной форме:
Чтобы получить уравнение траектории в координатной форме, надо из них исключить параметр t. Следует отметить, что в процессе движения точка может описывать не всю кривую, а только ее часть. Поэтому для определения траектории точки М необходимо задать пределы изменения ее координат в интервале времени движения. Если этот интервал не определен, то параметр времени изменяется в интервале Спроектируем равенство (2.2) на координатные оси. Учитывая (2.4), получаем
Здесь
– проекции вектора скорости на оси координат. Точку над буквой будем считать символом дифференцирования по времени. Таким образом, проекции скорости точки на координатные оси равны первым производным по времени от соответствующих переменных координат точки. Зная проекции скорости, найдем ее модуль и направление (т.е. углы α, β, γ, которые вектор
Вектор ускорения точки
или Проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения точки определяются по формулам
где В случае прямолинейного движения, которое задается одним уравнением
Естественный способ задания движения. Этим способом удобно пользоваться в тех случаях, когда траектория движущейся точки известна. Пусть точка М движется по некоторой криволинейной траектории (рис. 2.2). Выберем произвольный центр О за начало отсчета, а также положительное направление отсчета криволинейной координаты s. Положение точки М на траектории в любой момент времени можно определить, если задан закон движения точки в естественной форме,т.е. задан закон изменения координаты
Установим связь между естественным и координатным способами задания движения точки. В курсе дифференциальной геометрии доказано равенство
где
Первая производная по времени от криволинейной координаты называется алгебраической скоростью точки. Так как всегда
Естественными осями называют подвижную прямоугольную систему осей, направленных по касательной, главной нормали и бинормали к траектории. Эти оси, называемые осями естественного трехгранника, направлены следующим образом: ось Мτ; – по касательной к траектории в сторону положительного отсчета координаты  ; ось Мn – по нормали к траектории, лежащей в соприкасающейся плоскости М τ n и направленной в сторону вогнутости траектории; ось Мb – перпендикулярно к первым двум так, чтобы она образовала с ними правую систему осей (рис. 2.3). Орты  являются ортами касательной τ;, главной нормали n и бинормали b. Они перемещаются вместе с точкой  по траектории, изменяя свои направления.
Определение ускорения при естественном способе задания движения. Вектор скорости
Вектор Величина и направление второго слагаемого (2.13) зависит от производной Таким образом, вектор ускорения точки расположен в соприкасающейся плоскости и раскладывается на две взаимно перпендикулярные составляющие, одна из которых направлена по касательной к траектории точки, а вторая – по главной нормали к этой траектории в сторону вогнутости:
Составляющая ускорения в направлении бинормали равна нулю
Касательное ускорение определяет изменение величины (модуля) скорости. Если
Вектор  называется вектором нормального ускорения. Из (2.14) следует, что его модуль
Нормальное ускорение определяет изменение направления вектора скорости. Нормальное ускорение может быть равным нулю в трех случаях: 1) точка движется по прямой По составляющим
Получим еще одну формулу для определения модуля касательного ускорения. Из (2.7) имеем
Формулой (2.18) можно воспользоваться в случае, если движение точки задано координатным способом. Частные случаи движения точки. а) Равномерное движение. Движение точки с постоянной алгебраической скоростью называется равномерным. В этом случае
Ускорение в случае равномерного криволинейного движения точки равно нормальному ускорению б) Равнопеременное движение. Движение точки с постоянным по модулю касательным ускорением называется равнопеременным. Найдем закон изменения скорости и закон движения точки. Пусть при
Следовательно,
|
, проведенного из некоторого неподвижного центра О в данную точку М (рис. 2.1). Для определения движения точки нужно знать, как изменяется с течением времени радиус-вектор 
. (2.1)
− положение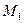 
, определяемое радиус-вектором 
. Отношение приращения радиус-вектора 
к промежутку времени 
, в течение которого произошло это перемещение, равно вектору средней скорости движения точки по хорде 
: 
.
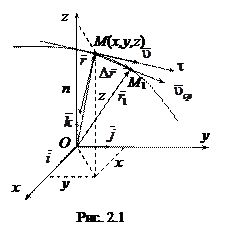
является величиной векторной и называется вектором скорости точки в момент времени t:
. (2.2)
направлен по хорде 
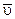направлен по касательной к траектории в сторону движения точки.
, то отношение 
, когда 
. Учитывая равенство (2.2), имеем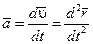
. (2.3)
, (2.4)
, 
, 
. (2.5)
.
или 
.
, 
, 
(2.6)
,
, 
, 
. (2.7)
. Отсюда на основании формул (2.3) и (2.4) получаем:
, 
, 
, 
, 
. (2.8)
, 
, 
, 
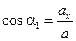, (2.9)
, 
, 
- углы, образуемые вектором ускорения с координатными осями.
, скорость и ускорение точки будут
, 
. (2.10)
. (2.11)
, где 
– элементарное перемещение точки вдоль дуги траектории за время 
, а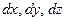 
- проекции элементарного перемещения на оси х, у, z. Разделим обе части равенства на 
,
– алгебраическая скорость точки:
. (2.12)
, то знак 
, то скорость направлена в сторону положительного отсчета координаты 
, то – в противоположную сторону.
в формулу (2.3), получаем
. (2.13)
направлен вдоль касательной в сторону возрастания координаты s при 
. При 
этот вектор направлен в противоположную сторону.
. Так как 
является вектором с постоянным модулем, его производная по скалярному аргументу t является вектором, перпендикулярным 
. Следовательно, 
. Предел отношения элементарного угла поворота касательной к длине соответствующей дуги кривой равен кривизне кривой k в данной точке или величине, обратной радиусу кривизны кривой ρ в данной точке: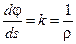 
.
. (2.14)
. Вектор 
называется вектором касательного ускорения. Алгебраическая величина касательного ускорения равна
или 
. (2.15)
, то скорость точки увеличивается – ее движение ускоренное и направления векторов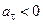 
, то скорость точки уменьшается – движение замедленное, направления векторов 
. (2.16)
; 2) в данный момент времени скорость точки равна нулю 
; 3) движущаяся точка находится в точке перегиба траектории 
.
и 
можно определить модуль ускорения:
. (2.17)
. Производная по времени от этого выражения 
. Отсюда
. (2.18)
, 
. Интегрируя выражение (2.12), получим 
, где С – постоянная интегрирования, определяемая из начального условия. Пусть при t = 0 координата точки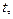 
. Следовательно, 
, и закон движения точки записывается так:
. (2.19)
. При прямолинейном равномерном движении ускорение равно нулю, т.к. 
.
начальная скорость 
и начальная координата 
. Так как 
, то согласно (2.15) 
. Интегрируя, получим 
. В свою очередь 
, и поэтому, с учетом выражения для 
. Постоянные интегрирования найдем из начальных условий. Для момента времени 
, 
.
, 
и выражения для 
, 
. 2.20)
