Приведение произвольной системы сил к данному центруЛемма Пуансо. Пусть сила
Далее заменим силы  и  моментом  (рис. 1.20,в). Окончательно получаем, что силу можно перенести параллельно в любую точку, не лежащую на линии ее действия, добавляя при этом пару сил с моментом, равным произведению одной из сил пары на плечо.
Сформулируем и докажем основную теорему статики. Пусть на абсолютно твердое тело действует произвольная система сил (рис. 1.21). Выберем произвольную точку О, которую назовем центром приведения. Перенесем параллельно силы
Векторную сумму системы присоединенных пар сил назовем главным моментом
Таким образом, любую систему сил, приложенных к абсолютно твердому телу можно заменить одной силой Теорема доказана. Заметим, что выбор центра приведения не отражается на модуле и направлении главного вектора
|
, полагая 
, 
, 
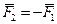(рис.1.20,б). Система сил 
образует пару, момент 
на плечо 
: 
.
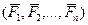в этот центр. Согласно лемме Пуансо, получим систему сходящихся в центре О сил 
, моменты которых равны моментам исходных сил относительно центра О: 
. Векторную сумму перенесенных в центр О сил назовем главным вектором
. (1.9)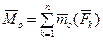
. (1.10)
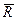, равной главному вектору, и одной парой сил с моментом 
, равным главному моменту исходной системы сил относительно центра О.
