Тело  массой
массой 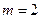 кг начинает движение в трубке
кг начинает движение в трубке  , расположенной в вертикальной плоскости, с начальной скоростью
, расположенной в вертикальной плоскости, с начальной скоростью  2,2 м/с под действием силы тяжести и силы
2,2 м/с под действием силы тяжести и силы  кН(рис.13).
кН(рис.13).
Длина участка 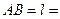 0,7м. Трением на участке
0,7м. Трением на участке  пренебречь. На участке
пренебречь. На участке 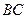 на тело кроме силы тяжести действует сила трения скольжения. Коэффициент трения f = 0,68. Сила
на тело кроме силы тяжести действует сила трения скольжения. Коэффициент трения f = 0,68. Сила  .
.
Определить скорость тела в точке
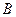
, время движения тела на участке
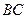
и длину участка
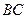
, предполагая, что
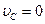
.
Решение. Сначала рассмотрим движение тела на участке  . Направим ось x вдоль
. Направим ось x вдоль  и составим дифференциальное уравнение движения тела на этом участке:
и составим дифференциальное уравнение движения тела на этом участке:
 ,
,
где  вес тела,
вес тела,  10 м/с2. Преобразуем ускорение к виду:
10 м/с2. Преобразуем ускорение к виду:
 . Вычислим
. Вычислим  sin45o =20Н – 2кг ∙;10м/с2 ∙;0,707 =
sin45o =20Н – 2кг ∙;10м/с2 ∙;0,707 =
= –5,86 Н. Имеем при  скорость
скорость  ; при
; при 
 . Разделяя переменные, интегрируем дифференциальное уравнение:
. Разделяя переменные, интегрируем дифференциальное уравнение:
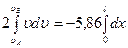 . Отсюда
. Отсюда  .
.
Скорость тела в точке 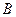 :
:  0,859 м/с.
0,859 м/с.
Теперь рассмотрим движение тела на участке 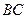 . Направим ось
. Направим ось 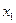 от точки
от точки 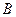 в сторону движения тела. На тело
в сторону движения тела. На тело  действуют силы:
действуют силы:  . Реакцию трубки
. Реакцию трубки  найдём из уравнения равновесия:
найдём из уравнения равновесия:  30о = 0,
30о = 0,  30о = 2 кг∙ 10 м/с2 ∙ 0,866 = = 17,32Н. По закону Кулона сила трения
30о = 2 кг∙ 10 м/с2 ∙ 0,866 = = 17,32Н. По закону Кулона сила трения 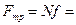 17,32 Н∙ 0,68 =
17,32 Н∙ 0,68 =
= 11,78 Н.
В начальном положении тела (в точке 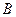 ) время
) время  0, координата
0, координата 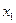 (0) = 0, скорость
(0) = 0, скорость  (0) =
(0) = 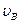 . В конечном положении тела (в точке
. В конечном положении тела (в точке  ) время
) время  , координата
, координата  и по условию задачи скорость
и по условию задачи скорость  .
.
Согласно второму закону динамики составим дифференциальное уравнение движения тела (материальной точки) в проекции на ось 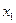 :
:
 .
.
Правая часть уравнения: 2 кг ∙ 10 м/с2∙ 0,5 –
– 11,78 Н= – 1,78 Н. Перенесём 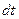 в правую часть и интегрируем:
в правую часть и интегрируем:
 , 2(
, 2( или
или  .
.
Заменив  на
на  = 0 и
= 0 и 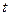 на
на  , найдём время движения тела на участке
, найдём время движения тела на участке 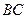 :
:  0,859/0,89 = 0,965 с. Скорость тела
0,859/0,89 = 0,965 с. Скорость тела  выразим через первую производную от координаты
выразим через первую производную от координаты 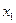 :
:  .
.
Перенесём 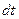 в правую часть и интегрируем
в правую часть и интегрируем
 . Отсюда
. Отсюда  = 0,415 м.
= 0,415 м.
Ответ: 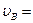 0,859 м/с,
0,859 м/с,  0,965 с,
0,965 с,  0,415 м.
0,415 м.
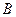 , время движения тела на участке
, время движения тела на участке 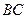 и длину участка
и длину участка 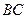 , предполагая, что
, предполагая, что 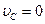 .
.

 массой
массой 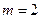 кг начинает движение в трубке
кг начинает движение в трубке  , расположенной в вертикальной плоскости, с начальной скоростью
, расположенной в вертикальной плоскости, с начальной скоростью  2,2 м/с под действием силы тяжести и силы
2,2 м/с под действием силы тяжести и силы  кН(рис.13).
кН(рис.13).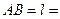 0,7м. Трением на участке
0,7м. Трением на участке  пренебречь. На участке
пренебречь. На участке  .
.
 ,
, вес тела,
вес тела,  10 м/с2. Преобразуем ускорение к виду:
10 м/с2. Преобразуем ускорение к виду: . Вычислим
. Вычислим  sin45o =20Н – 2кг ∙;10м/с2 ∙;0,707 =
sin45o =20Н – 2кг ∙;10м/с2 ∙;0,707 = скорость
скорость  ; при
; при 
 . Разделяя переменные, интегрируем дифференциальное уравнение:
. Разделяя переменные, интегрируем дифференциальное уравнение: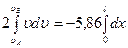 . Отсюда
. Отсюда  .
. 0,859 м/с.
0,859 м/с.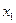 от точки
от точки  . Реакцию трубки
. Реакцию трубки  найдём из уравнения равновесия:
найдём из уравнения равновесия:  30о = 0,
30о = 0,  30о = 2 кг∙ 10 м/с2 ∙ 0,866 = = 17,32Н. По закону Кулона сила трения
30о = 2 кг∙ 10 м/с2 ∙ 0,866 = = 17,32Н. По закону Кулона сила трения 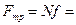 17,32 Н∙ 0,68 =
17,32 Н∙ 0,68 = 0, координата
0, координата  (0) =
(0) = 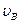 . В конечном положении тела (в точке
. В конечном положении тела (в точке  ) время
) время  , координата
, координата  и по условию задачи скорость
и по условию задачи скорость  .
. .
.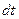 в правую часть и интегрируем:
в правую часть и интегрируем: , 2(
, 2( или
или  .
. = 0 и
= 0 и 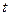 на
на  , найдём время движения тела на участке
, найдём время движения тела на участке  0,859/0,89 = 0,965 с. Скорость тела
0,859/0,89 = 0,965 с. Скорость тела  .
. . Отсюда
. Отсюда  = 0,415 м.
= 0,415 м.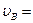 0,859 м/с,
0,859 м/с,  0,415 м.
0,415 м.


