Механическая система состоит из прямоугольной плиты массой 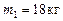 , движущейся в вертикальной плоскости вдоль горизонтальных направляющих с начальной скоростью
, движущейся в вертикальной плоскости вдоль горизонтальных направляющих с начальной скоростью 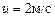 , и груза
, и груза  массой
массой  . Груз начинает движение из центра масс плиты
. Груз начинает движение из центра масс плиты  вдоль жёлоба по закону
вдоль жёлоба по закону  =
=  м. На рис.16 груз
м. На рис.16 груз 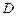 показан в положении
показан в положении  > 0 (при
> 0 (при  < 0 груз
< 0 груз  находится по другую сторону от точки
находится по другую сторону от точки  ).
).
Пренебрегая всеми сопротивлениями движению, определить: перемещение 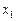 плиты за время
плиты за время  с; нормальную реакцию
с; нормальную реакцию  горизонтальных направляющих при
горизонтальных направляющих при  с.
с.
 Решение. На рис.16 плита и груз показаны в момент времени
Решение. На рис.16 плита и груз показаны в момент времени 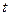 . Оси координат
. Оси координат  проведём так, чтобы при
проведём так, чтобы при 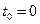 ось
ось  проходила через центр плиты
проходила через центр плиты  . Здесь
. Здесь 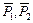 – силы тяжести плиты и груза;
– силы тяжести плиты и груза;  реакция горизонтальных направляющих;
реакция горизонтальных направляющих;  вектор скорости плиты;
вектор скорости плиты;  координата центра масс плиты;
координата центра масс плиты;
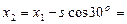
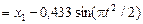 – координата груза
– координата груза  . Обозначим через
. Обозначим через  координату центра масс систе-
координату центра масс систе-
мы. Масса системы M = m1+m2 = 24 кг. Координата центра масс системы определяется по формуле:
 ,
,
24  = 18
= 18 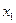 + 6
+ 6 
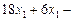 2,60 sin(πt2/2) = 24
2,60 sin(πt2/2) = 24  2,60 sin(πt2/2).
2,60 sin(πt2/2).
Отсюда
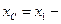 0,108 sin(πt2/2). (3)
0,108 sin(πt2/2). (3)
Проекция скорости центра масс на ось  будет
будет
 0,108 πt cos(πt2/2). (4)
0,108 πt cos(πt2/2). (4)
По теореме о движении центра масс системы в проекции на ось  :
:
 или
или  .
.
Интегрируя дважды это выражение, получим:
 ,
,  . (5)
. (5)
Приравниваем, соответственно, правые части (3), (4) и (5):
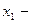 0,108 sin(πt2/2) =
0,108 sin(πt2/2) = 
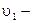 0,108 πt cos(πt2/2) =
0,108 πt cos(πt2/2) =  . (6)
. (6)
Определим постоянные интегрирования  по начальным условиям:
по начальным условиям:  (0)
(0)  2м/с,
2м/с, 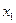 (0) = 0. Подставляя эти значения в (6), найдём:
(0) = 0. Подставляя эти значения в (6), найдём:  2м/с,
2м/с,  . Заменив в (6)
. Заменив в (6)  их значениями, получим выражение для скорости плиты и её закон движения:
их значениями, получим выражение для скорости плиты и её закон движения:
 0,108 πt cos(πt2/2),
0,108 πt cos(πt2/2),  0,108 sin(πt2/2).
0,108 sin(πt2/2).
Перемещение плиты в момент времени  с будет
с будет
 2,108 м ≈ 2,11 м.
2,108 м ≈ 2,11 м.
Определим нормальную реакцию горизонтальных направляющих. Координата 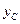 центра масс системы определяется по формуле:
центра масс системы определяется по формуле:
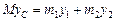 , (7)
, (7)
где координата центра масс плиты  при движении плиты не меняется, координата груза
при движении плиты не меняется, координата груза  0,25 sin(πt2/2).
0,25 sin(πt2/2).
Теорема о движении центра масс системы в проекции на ось  :
:

 . (8)
. (8)
Дважды продифференцируем уравнение (7):

 ,
,

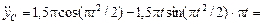
 . (9)
. (9)
Приравнивая правые части (8) и (9), найдём реакцию  :
:

 .
.
В момент времени  с
с

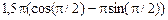 =
= 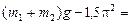
 Н.
Н.
Ответ:  м;
м; 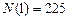 Н.
Н.

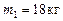 , движущейся в вертикальной плоскости вдоль горизонтальных направляющих с начальной скоростью
, движущейся в вертикальной плоскости вдоль горизонтальных направляющих с начальной скоростью 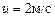 , и груза
, и груза  массой
массой  . Груз начинает движение из центра масс плиты
. Груз начинает движение из центра масс плиты  вдоль жёлоба по закону
вдоль жёлоба по закону  =
=  м. На рис.16 груз
м. На рис.16 груз 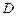 показан в положении
показан в положении  > 0 (при
> 0 (при 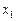 плиты за время
плиты за время  с; нормальную реакцию
с; нормальную реакцию  горизонтальных направляющих при
горизонтальных направляющих при  Решение. На рис.16 плита и груз показаны в момент времени
Решение. На рис.16 плита и груз показаны в момент времени 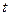 . Оси координат
. Оси координат  проведём так, чтобы при
проведём так, чтобы при 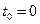 ось
ось  проходила через центр плиты
проходила через центр плиты  . Здесь
. Здесь 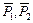 – силы тяжести плиты и груза;
– силы тяжести плиты и груза;  реакция горизонтальных направляющих;
реакция горизонтальных направляющих;  вектор скорости плиты;
вектор скорости плиты;  координата центра масс плиты;
координата центра масс плиты;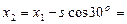
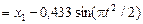 – координата груза
– координата груза  координату центра масс систе-
координату центра масс систе- ,
, = 18
= 18 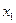 + 6
+ 6 
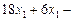 2,60 sin(πt2/2) = 24
2,60 sin(πt2/2) = 24 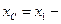 0,108 sin(πt2/2). (3)
0,108 sin(πt2/2). (3) будет
будет 0,108 πt cos(πt2/2). (4)
0,108 πt cos(πt2/2). (4) :
: или
или  .
. ,
,  . (5)
. (5)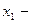 0,108 sin(πt2/2) =
0,108 sin(πt2/2) = 
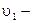 0,108 πt cos(πt2/2) =
0,108 πt cos(πt2/2) =  . (6)
. (6) по начальным условиям:
по начальным условиям:  (0)
(0)  2м/с,
2м/с,  2м/с,
2м/с,  . Заменив в (6)
. Заменив в (6)  их значениями, получим выражение для скорости плиты и её закон движения:
их значениями, получим выражение для скорости плиты и её закон движения: 0,108 πt cos(πt2/2),
0,108 πt cos(πt2/2),  0,108 sin(πt2/2).
0,108 sin(πt2/2). 2,108 м ≈ 2,11 м.
2,108 м ≈ 2,11 м.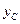 центра масс системы определяется по формуле:
центра масс системы определяется по формуле: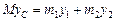 , (7)
, (7) при движении плиты не меняется, координата груза
при движении плиты не меняется, координата груза  0,25 sin(πt2/2).
0,25 sin(πt2/2). :
:
 . (8)
. (8) ,
,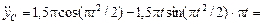
 . (9)
. (9) :
:
 .
.
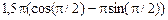 =
= 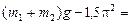
 Н.
Н. м;
м;  Н.
Н.


