Задача №8. По ободу диска радиуса R (рис
Дано: R =30 см; φ = Решение. Абсолютное движение точки М складывается из относительного движения точки по ободу диска, заданного естественным способом по закону s = Неподвижную систему координат О 1 х 1 у 1 z 1 свяжем с опорой О 1 (рис. 12), ось z 1 направим по диаметру диска, вокруг которого он вращается, а подвижную систему координат Вычислим переносную угловую скорость и переносное угловое ускорение диска: ,. В заданный момент времени t 1=1c Определим положение точки М в момент времени t 1= 1с
Центральный угол, включающий дугу s 1, вычислим по формуле
Для определения переносной скорости 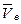 и переносного ускорения и переносного ускорения 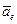 мысленно остановим относительное движение точки в момент времени t 1 = 1с и определим скорость и ускорение той точки т диска (рис. 12), где в данный момент находится движущаяся точка мысленно остановим относительное движение точки в момент времени t 1 = 1с и определим скорость и ускорение той точки т диска (рис. 12), где в данный момент находится движущаяся точка 
. Расстояние h = МК отсчитывается от точки М до оси вращения
Вектор переносной скорости Переносное ускорение раскладываем на касательную и нормальную составляющие
где модули составляющих Вектор касательного ускорения Перейдем к вычислению относительной скорости и относительного ускорения точки М. Мысленно остановим переносное вращательное движение диска. Относительное движение точки М задано естественным способом. Выберем естественные оси ее траектории. Направим единичный вектор касательной Определим относительную скорость:
Для момента времени t 1= 1с См/с2. Проекция относительной скорости на касательную положительна, следовательно, направление вектора Относительное ускорение
где
Поскольку Кориолисово ускорение
Модуль Кориолисова ускорения в момент времени t 1 = 1с равен
Вектор Кориолисова ускорения по правилу векторного произведения направлен, в данном случае, параллельно оси О 1 х 1 в сторону положительного направления оси Абсолютную скорость точки М вычислим по теореме сложения скоростей (2.32):
Так как векторы
Абсолютное ускорение точки М вычислим по теореме Кориолиса (2.33): . Эти векторы проектируем на неподвижные оси координат О 1 х 1 у 1 z 1
Модуль абсолютного ускорения точки М
|

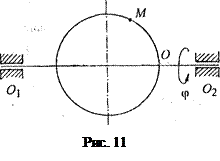
 рад; s =
рад; s =  см; t 1 = 1c.
см; t 1 = 1c.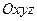 свяжем с диском (система на рисунке не показана). Считаем, что плоскость диска в данный момент времени совпадает с плоскостью О 1 у 1 z 1.
свяжем с диском (система на рисунке не показана). Считаем, что плоскость диска в данный момент времени совпадает с плоскостью О 1 у 1 z 1. рад/си, следовательно, диск вращается равноускоренно с угловой скоростью
рад/си, следовательно, диск вращается равноускоренно с угловой скоростью  рад/с и угловым ускорением
рад/с и угловым ускорением  рад/с2 в сторону, противоположную положительному направлению отсчета угла поворота (рис. 12).
рад/с2 в сторону, противоположную положительному направлению отсчета угла поворота (рис. 12).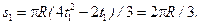
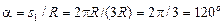 .
.
 диска. Из прямоугольного треугольника СМК расстояние
диска. Из прямоугольного треугольника СМК расстояние 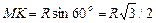 . Тогда переносная скорость будет равна
. Тогда переносная скорость будет равна см/с.
см/с.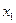 .
.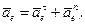
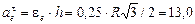 см/с2,
см/с2,  см/с2.
см/с2. направим в сторону дуговой стрелки углового ускорения. Его направление совпадает с направлением переносной скорости
направим в сторону дуговой стрелки углового ускорения. Его направление совпадает с направлением переносной скорости  направим по прямой МК к оси вращения.
направим по прямой МК к оси вращения. в сторону положительного отсчета координаты s, а единичный вектор нормали
в сторону положительного отсчета координаты s, а единичный вектор нормали 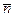 –кцентру окружности (рис. 12).
–кцентру окружности (рис. 12).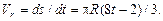
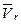 совпадает c направлением единичного вектора
совпадает c направлением единичного вектора  при криволинейном движении точки раскладывается на касательную и нормальную составляющие
при криволинейном движении точки раскладывается на касательную и нормальную составляющие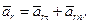
 см/с2,
см/с2, см/с2.
см/с2.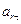 >0, то направление вектора
>0, то направление вектора  совпадает с направлением единичного вектора
совпадает с направлением единичного вектора  определим по формуле (2.34):
определим по формуле (2.34): .
. см/с2.
см/с2.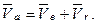
 см/с = 1,89 см/с2.
см/с = 1,89 см/с2. см/с2,
см/с2,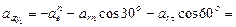
 см/с2,
см/с2, см/с2.
см/с2. м/с2.
м/с2.


