
Плоская рама  (рис.1) закреплена в точке
(рис.1) закреплена в точке 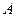 шарнирно неподвижной опорой, а в точке
шарнирно неподвижной опорой, а в точке  – невесомым стержнем
– невесомым стержнем  с шарнирами на концах. На раму действуют: пара сил с моментом
с шарнирами на концах. На раму действуют: пара сил с моментом  , силы
, силы  и равномерно распределённая нагрузка интенсивности
и равномерно распределённая нагрузка интенсивности  . Дано:
. Дано:  кН;
кН;  кН;
кН; 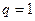 кН/м;
кН/м; 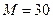 кН∙м;
кН∙м;  м;
м;  м;
м;  м.
м.
Определить реакции в точках 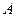 и
и  .
.
Рис.1 Рис.2
Решение. Изображаем раму свободной в точках 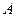 и
и  от связей (рис.2), а их действие заменяем реакциями
от связей (рис.2), а их действие заменяем реакциями  . Реакцию
. Реакцию  (она на рисунке не показана) раскладываем на составляющие
(она на рисунке не показана) раскладываем на составляющие 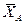 ,
,  . Реакцию
. Реакцию  направим вдоль невесомого стержня
направим вдоль невесомого стержня  . Распределённую нагрузку заменяем равнодействующей
. Распределённую нагрузку заменяем равнодействующей 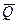 , приложенной посредине отрезка
, приложенной посредине отрезка  , величиной
, величиной 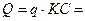 1 кН/м
1 кН/м 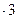 м =
м = 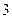 кН. Силы
кН. Силы  раскладываем на составляющие, параллельные осям
раскладываем на составляющие, параллельные осям  . Модули этих составляющих:
. Модули этих составляющих:  = 1 кН∙0,966 = 0,966кН,
= 1 кН∙0,966 = 0,966кН, 
=  кН∙0,259 = 0,259 кН;
кН∙0,259 = 0,259 кН;  2 кН ∙0,866 = 1,73 кН,
2 кН ∙0,866 = 1,73 кН,
 2 кН∙0,5 = 1 кН. Направления составляющих показаны на рис.2. Рама находится в равновесии под действием произвольной плоской системы сил. Составим уравнения равновесия:
2 кН∙0,5 = 1 кН. Направления составляющих показаны на рис.2. Рама находится в равновесии под действием произвольной плоской системы сил. Составим уравнения равновесия:
1) 

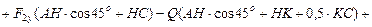
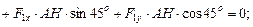
2) 

3) 

Из уравнения 1) находим:


Из уравнений 2) и 3) определяем:

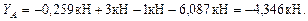
Можно сделать проверку, составив дополнительное уравнение, которое должно обратиться в тождество вида  с погрешностью вычислений, не превышающей 1%. Таким уравнением может быть, например,
с погрешностью вычислений, не превышающей 1%. Таким уравнением может быть, например,
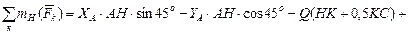
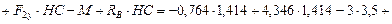
 кН∙м.
кН∙м.
Относительная погрешность: 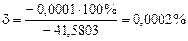 <
<  .
.
Ответ:  кН,
кН,  кН,
кН,  кН.
кН.
Знаки «минус» указывают, что силы  и
и  направлены противоположно показанным на рис. 2. Модуль реакции в точке
направлены противоположно показанным на рис. 2. Модуль реакции в точке 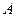 будет:
будет:  кН.
кН.


 (рис.1) закреплена в точке
(рис.1) закреплена в точке 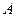 шарнирно неподвижной опорой, а в точке
шарнирно неподвижной опорой, а в точке  – невесомым стержнем
– невесомым стержнем  с шарнирами на концах. На раму действуют: пара сил с моментом
с шарнирами на концах. На раму действуют: пара сил с моментом  , силы
, силы  и равномерно распределённая нагрузка интенсивности
и равномерно распределённая нагрузка интенсивности  . Дано:
. Дано:  кН;
кН;  кН;
кН; 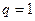 кН/м;
кН/м; 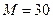 кН∙м;
кН∙м;  м;
м;  м;
м;  м.
м. . Реакцию
. Реакцию  (она на рисунке не показана) раскладываем на составляющие
(она на рисунке не показана) раскладываем на составляющие 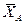 ,
,  . Реакцию
. Реакцию  направим вдоль невесомого стержня
направим вдоль невесомого стержня 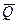 , приложенной посредине отрезка
, приложенной посредине отрезка  , величиной
, величиной 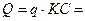 1 кН/м
1 кН/м 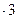 м =
м = 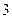 кН. Силы
кН. Силы  . Модули этих составляющих:
. Модули этих составляющих:  = 1 кН∙0,966 = 0,966кН,
= 1 кН∙0,966 = 0,966кН, 
 кН∙0,259 = 0,259 кН;
кН∙0,259 = 0,259 кН;  2 кН ∙0,866 = 1,73 кН,
2 кН ∙0,866 = 1,73 кН, 2 кН∙0,5 = 1 кН. Направления составляющих показаны на рис.2. Рама находится в равновесии под действием произвольной плоской системы сил. Составим уравнения равновесия:
2 кН∙0,5 = 1 кН. Направления составляющих показаны на рис.2. Рама находится в равновесии под действием произвольной плоской системы сил. Составим уравнения равновесия:

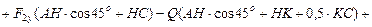
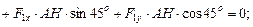







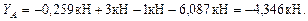
 с погрешностью вычислений, не превышающей 1%. Таким уравнением может быть, например,
с погрешностью вычислений, не превышающей 1%. Таким уравнением может быть, например,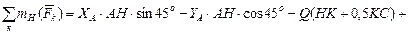
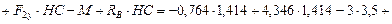
 кН∙м.
кН∙м.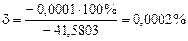 <
<  .
. кН,
кН,  кН,
кН,  кН.
кН. и
и  направлены противоположно показанным на рис. 2. Модуль реакции в точке
направлены противоположно показанным на рис. 2. Модуль реакции в точке  кН.
кН.


