Контрольная работа №2
Тема 5: «Интегрирование дифференциальных уравнений движения материальной точки»
Задача Д- 1
По последней цифре шифра следует выбрать номер схемы, а по предпоследней – номер строки Таблицы Д-1.
Таблица Д-1
| № строки
|  , м/с , м/с
|  , Н , Н
|  , м , м
| № строки
|  , м/с , м/с
|  , Н , Н
|  , м , м
|
|
| 2,0
|
| 1,0
|
| 1,6
|
| 0,2
|
|
| 2,5
|
| 0,6
|
| 1,4
|
| 0,5
|
|
| 1,2
|
| 0,8
|
| 2,2
|
| 0,7
|
|
| 1,6
|
| 0,4
|
| 2,4
|
| 0,9
|
|
| 1,8
|
| 0,3
|
| 2,6
|
| 1,2
|
Схемы к задаче Д- 1

Условие задачи
Тело 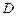 массой
массой  2 кг начинает движение с начальной скоростью
2 кг начинает движение с начальной скоростью  в изогнутой трубке
в изогнутой трубке  , расположенной в вертикальной плоскости. На участке
, расположенной в вертикальной плоскости. На участке 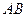 длиной
длиной  на тело, кроме силы тяжести, действует постоянная сила
на тело, кроме силы тяжести, действует постоянная сила  , направленная вдоль трубки от
, направленная вдоль трубки от  к
к  .
.
Трением на этом участке пренебречь. В точке  тело
тело 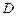 , не меняя величины скорости, переходит на участок
, не меняя величины скорости, переходит на участок  . При движении на этом участке на тело, кроме силы тяжести, действует сила трения скольжения с коэффициентом трения
. При движении на этом участке на тело, кроме силы тяжести, действует сила трения скольжения с коэффициентом трения  0,8, где
0,8, где  0. Считая движение тела поступательным (т.е. тело считать материальной точкой), определить скорость тела в положении
0. Считая движение тела поступательным (т.е. тело считать материальной точкой), определить скорость тела в положении  , время движения на участке
, время движения на участке  и длину участка
и длину участка  , предполагая, что в точке
, предполагая, что в точке  тело остановилось (
тело остановилось ( 0).
0).
Указания к решению задачи Д- 1
Решение задачи следует разбить на два этапа. Сначала надо направить ось 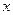 в сторону движения точки (от
в сторону движения точки (от 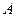 к
к  ), составить дифференциальное уравнение движения тела
), составить дифференциальное уравнение движения тела 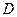 на участке
на участке 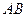 , умножить обе части уравнения на
, умножить обе части уравнения на  и проинтегрировать полученное уравнение. В результате получится зависимость между скоростью
и проинтегрировать полученное уравнение. В результате получится зависимость между скоростью  и координатой
и координатой 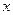 . Подставив в эту зависимость
. Подставив в эту зависимость  , получим численное значение скорости
, получим численное значение скорости  .
.
Затем следует направить ось  в направлении
в направлении  , составить и дважды проинтегрировать дифференциальное уравнение движения тела
, составить и дважды проинтегрировать дифференциальное уравнение движения тела 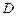 на участке
на участке  . В результате первого интегрирования получим зависимость между скоростью
. В результате первого интегрирования получим зависимость между скоростью  и временем
и временем 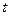 . Учитывая, что
. Учитывая, что  0, найдём
0, найдём  – время движения тела на участке
– время движения тела на участке  .
.
В результате повторного интегрирования получим зависимость между координатой 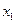 и временем
и временем 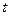 . Подставив
. Подставив 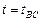 , найдем длину участка
, найдем длину участка  .
.
Тема 6: «Общие теоремы динамики точки»
Задача Д- 2
По последней цифре шифра следует выбрать условие задачи и номер схемы, а по предпоследней – номер столбца соответствующей таблицы. Например, по шифру 73 нужно решать задачу Д-2.3 (рис.Д-2.3) и данные взять из 7-го столбца таблицы Д-2.3.

 , м/с
, м/с
 , Н
, Н
 , м
, м


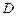 массой
массой  2 кг начинает движение с начальной скоростью
2 кг начинает движение с начальной скоростью  в изогнутой трубке
в изогнутой трубке  , расположенной в вертикальной плоскости. На участке
, расположенной в вертикальной плоскости. На участке 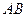 длиной
длиной  к
к  .
. . При движении на этом участке на тело, кроме силы тяжести, действует сила трения скольжения с коэффициентом трения
. При движении на этом участке на тело, кроме силы тяжести, действует сила трения скольжения с коэффициентом трения  0,8, где
0,8, где  0. Считая движение тела поступательным (т.е. тело считать материальной точкой), определить скорость тела в положении
0. Считая движение тела поступательным (т.е. тело считать материальной точкой), определить скорость тела в положении  и длину участка
и длину участка  тело остановилось (
тело остановилось ( 0).
0).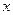 в сторону движения точки (от
в сторону движения точки (от 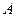 к
к  ), составить дифференциальное уравнение движения тела
), составить дифференциальное уравнение движения тела 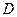 на участке
на участке  и проинтегрировать полученное уравнение. В результате получится зависимость между скоростью
и проинтегрировать полученное уравнение. В результате получится зависимость между скоростью  и координатой
и координатой  , получим численное значение скорости
, получим численное значение скорости  .
. в направлении
в направлении  и временем
и временем 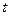 . Учитывая, что
. Учитывая, что  0, найдём
0, найдём  – время движения тела на участке
– время движения тела на участке 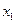 и временем
и временем 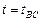 , найдем длину участка
, найдем длину участка 


