Задача Д-3.0. Задача решается с помощью теоремы об изменении кинетического момента механической системы относительно точки  :
:  . Кинетический момент системы состоит из кинетического момента барабана и кинетического момента груза
. Кинетический момент системы состоит из кинетического момента барабана и кинетического момента груза 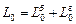 . Кинетический момент
. Кинетический момент 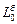 вычисляется по формуле кинетического момента вращающегося твёрдого тела, а
вычисляется по формуле кинетического момента вращающегося твёрдого тела, а 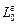 – по формуле кинетического момента точки (груз
– по формуле кинетического момента точки (груз 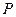 принимаем за материальную точку). По ходу решения задачи получаем угловое ускорение
принимаем за материальную точку). По ходу решения задачи получаем угловое ускорение 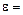 const, т.е. барабан вращается равноускоренно. Тогда угол поворота
const, т.е. барабан вращается равноускоренно. Тогда угол поворота  , измеряемый в радианах. Число оборотов определяется по формуле
, измеряемый в радианах. Число оборотов определяется по формуле 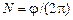 .
.
Задача Д-3.1. Задача решается в два этапа. На первом этапе следует применить теорему об изменении количества движения системы  в проекции на ось
в проекции на ось 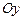 . Проекция количества движения системы
. Проекция количества движения системы 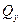 на ось
на ось 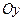 складывается из проекций количеств движения грузов. Количество движения барабана равно нулю, т.к. центр тяжести барабана находится в покое. Проекции внешних сил складываются из сил тяжести грузов, барабана и реакции опоры.
складывается из проекций количеств движения грузов. Количество движения барабана равно нулю, т.к. центр тяжести барабана находится в покое. Проекции внешних сил складываются из сил тяжести грузов, барабана и реакции опоры.
На втором этапе для определения ускорения грузов применяется теорема об изменении кинетического момента системы относительно точки 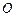 :
: 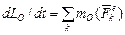 .
.
Задача Д-3.2. На систему действуют силы тяжести 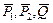 , вращающий момент
, вращающий момент 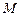 и реакции опоры
и реакции опоры  . Реакции опоры можно не определять, если применить теорему об изменении кинетического момента относительно оси, проходящей через центр
. Реакции опоры можно не определять, если применить теорему об изменении кинетического момента относительно оси, проходящей через центр 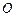 :
: 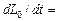
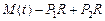 . Интегрируя это дифференциальное уравнение, получим
. Интегрируя это дифференциальное уравнение, получим  . С другой стороны кинетический момент данной системы равняется
. С другой стороны кинетический момент данной системы равняется 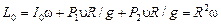
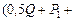
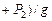 . Определив постоянную интегрирования при
. Определив постоянную интегрирования при 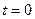 по начальной скорости
по начальной скорости 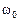 , можно найти угловую скорость при
, можно найти угловую скорость при 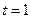 с.
с.
Задача Д-3.3. Рекомендуется применить теорему об изменении количества движения механической системы в проекции на ось 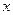 , где за ось
, где за ось 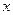 принята прямая, по которой движется балка
принята прямая, по которой движется балка 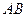 . При определении главного вектора количеств движения на ось
. При определении главного вектора количеств движения на ось 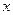 необходимо учесть, что скорость тележки состоит из переносной скорости балки и относительной скорости тележки, определяемой по уравнению
необходимо учесть, что скорость тележки состоит из переносной скорости балки и относительной скорости тележки, определяемой по уравнению  . Внешними силами являются силы трения между балкой и опорами.
. Внешними силами являются силы трения между балкой и опорами.
Задача Д-3.4. На системудействуют внешние силы: 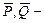 силы тяжести стержня и груза;
силы тяжести стержня и груза; 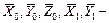 реакции опор в точках
реакции опор в точках 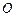 и
и 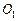 ;
;  вращающий момент. Чтобы не учитывать реакции опор, рекомендуется применить теорему об изменении кинетического момента системы относительно оси вращения:
вращающий момент. Чтобы не учитывать реакции опор, рекомендуется применить теорему об изменении кинетического момента системы относительно оси вращения: 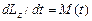 . Далее действовать по схеме, рекомендованной в задаче Д-3.2. Моменты инерции стержня и материальной точки определяются по известным формулам.
. Далее действовать по схеме, рекомендованной в задаче Д-3.2. Моменты инерции стержня и материальной точки определяются по известным формулам.
Задача Д-3.5. См. указания к задаче Д-3.4.
Задача Д-3.6. Ход решения задачи совпадает с Д-3.5. Здесь следует учесть, что момент инерции диска относительно оси вращения определяется формулой Гюйгенса-Штейнера: 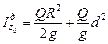 . Момент инерции груза
. Момент инерции груза 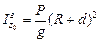 , если груз находится в точке
, если груз находится в точке 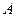 . Естественно, что
. Естественно, что 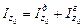 .
.
Задачи Д-3.7–Д-3.9. На механическую систему действуют внешние силы:  силы тяжести плиты и груза;
силы тяжести плиты и груза; 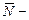 реакция горизонтальных направляющих, численно равная давлению плиты на эти направляющие. Сумма проекций всех сил на ось
реакция горизонтальных направляющих, численно равная давлению плиты на эти направляющие. Сумма проекций всех сил на ось 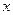 равна нулю. Тогда проекция главного вектора количеств движения на ось
равна нулю. Тогда проекция главного вектора количеств движения на ось 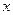 постоянна:
постоянна: 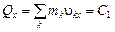 . Здесь
. Здесь 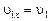 , а проекция абсолютной скорости груза на ось
, а проекция абсолютной скорости груза на ось 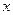 складывается из переносной скорости плиты
складывается из переносной скорости плиты 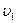 и проекции на ось
и проекции на ось 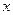 относительной скорости груза, определяемой по заданному закону
относительной скорости груза, определяемой по заданному закону 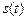 . Необходимо найти
. Необходимо найти 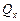 в момент времени
в момент времени 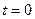 и в произвольный момент времени
и в произвольный момент времени 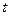 . Так как
. Так как 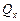 постоянна, то приравнивая правые части полученных выражений, найдем скорость плиты
постоянна, то приравнивая правые части полученных выражений, найдем скорость плиты 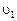 как функцию времени. Дифференцируя это уравнение, получим ускорение
как функцию времени. Дифференцируя это уравнение, получим ускорение 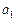 плиты. Интегрируя это уравнение, найдем закон движения плиты
плиты. Интегрируя это уравнение, найдем закон движения плиты 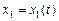 . По начальному условию
. По начальному условию 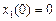 определяем постоянную интегрирования
определяем постоянную интегрирования  . Подставляя в полученные уравнения
. Подставляя в полученные уравнения 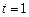 с, найдем искомые величины.
с, найдем искомые величины.
Для определения силы нормального давления плиты 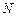 на направляющие следует применить теорему об изменении количества движения механической системы в проекции на ось
на направляющие следует применить теорему об изменении количества движения механической системы в проекции на ось 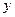 (см. указания к задаче Д-3.1) или применить теорему о движении центра масс системы (см. пример решения задачи №12).
(см. указания к задаче Д-3.1) или применить теорему о движении центра масс системы (см. пример решения задачи №12).

 :
:  . Кинетический момент системы состоит из кинетического момента барабана и кинетического момента груза
. Кинетический момент системы состоит из кинетического момента барабана и кинетического момента груза 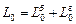 . Кинетический момент
. Кинетический момент 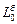 вычисляется по формуле кинетического момента вращающегося твёрдого тела, а
вычисляется по формуле кинетического момента вращающегося твёрдого тела, а 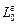 – по формуле кинетического момента точки (груз
– по формуле кинетического момента точки (груз 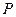 принимаем за материальную точку). По ходу решения задачи получаем угловое ускорение
принимаем за материальную точку). По ходу решения задачи получаем угловое ускорение 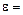 const, т.е. барабан вращается равноускоренно. Тогда угол поворота
const, т.е. барабан вращается равноускоренно. Тогда угол поворота  , измеряемый в радианах. Число оборотов определяется по формуле
, измеряемый в радианах. Число оборотов определяется по формуле 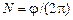 .
. в проекции на ось
в проекции на ось 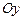 . Проекция количества движения системы
. Проекция количества движения системы 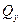 на ось
на ось 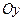 складывается из проекций количеств движения грузов. Количество движения барабана равно нулю, т.к. центр тяжести барабана находится в покое. Проекции внешних сил складываются из сил тяжести грузов, барабана и реакции опоры.
складывается из проекций количеств движения грузов. Количество движения барабана равно нулю, т.к. центр тяжести барабана находится в покое. Проекции внешних сил складываются из сил тяжести грузов, барабана и реакции опоры.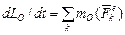 .
.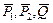 , вращающий момент
, вращающий момент 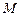 и реакции опоры
и реакции опоры  . Реакции опоры можно не определять, если применить теорему об изменении кинетического момента относительно оси, проходящей через центр
. Реакции опоры можно не определять, если применить теорему об изменении кинетического момента относительно оси, проходящей через центр 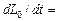
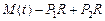 . Интегрируя это дифференциальное уравнение, получим
. Интегрируя это дифференциальное уравнение, получим  . С другой стороны кинетический момент данной системы равняется
. С другой стороны кинетический момент данной системы равняется 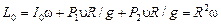
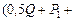
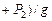 . Определив постоянную интегрирования при
. Определив постоянную интегрирования при 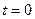 по начальной скорости
по начальной скорости 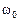 , можно найти угловую скорость при
, можно найти угловую скорость при 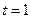 с.
с.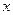 , где за ось
, где за ось 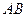 . При определении главного вектора количеств движения на ось
. При определении главного вектора количеств движения на ось  . Внешними силами являются силы трения между балкой и опорами.
. Внешними силами являются силы трения между балкой и опорами.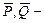 силы тяжести стержня и груза;
силы тяжести стержня и груза; 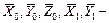 реакции опор в точках
реакции опор в точках 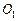 ;
;  вращающий момент. Чтобы не учитывать реакции опор, рекомендуется применить теорему об изменении кинетического момента системы относительно оси вращения:
вращающий момент. Чтобы не учитывать реакции опор, рекомендуется применить теорему об изменении кинетического момента системы относительно оси вращения: 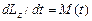 . Далее действовать по схеме, рекомендованной в задаче Д-3.2. Моменты инерции стержня и материальной точки определяются по известным формулам.
. Далее действовать по схеме, рекомендованной в задаче Д-3.2. Моменты инерции стержня и материальной точки определяются по известным формулам.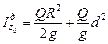 . Момент инерции груза
. Момент инерции груза 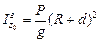 , если груз находится в точке
, если груз находится в точке 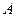 . Естественно, что
. Естественно, что 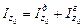 .
. силы тяжести плиты и груза;
силы тяжести плиты и груза; 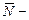 реакция горизонтальных направляющих, численно равная давлению плиты на эти направляющие. Сумма проекций всех сил на ось
реакция горизонтальных направляющих, численно равная давлению плиты на эти направляющие. Сумма проекций всех сил на ось 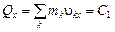 . Здесь
. Здесь 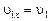 , а проекция абсолютной скорости груза на ось
, а проекция абсолютной скорости груза на ось 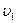 и проекции на ось
и проекции на ось 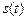 . Необходимо найти
. Необходимо найти 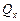 в момент времени
в момент времени 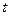 . Так как
. Так как 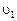 как функцию времени. Дифференцируя это уравнение, получим ускорение
как функцию времени. Дифференцируя это уравнение, получим ускорение 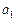 плиты. Интегрируя это уравнение, найдем закон движения плиты
плиты. Интегрируя это уравнение, найдем закон движения плиты 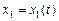 . По начальному условию
. По начальному условию 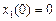 определяем постоянную интегрирования
определяем постоянную интегрирования  . Подставляя в полученные уравнения
. Подставляя в полученные уравнения 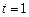 с, найдем искомые величины.
с, найдем искомые величины. на направляющие следует применить теорему об изменении количества движения механической системы в проекции на ось
на направляющие следует применить теорему об изменении количества движения механической системы в проекции на ось 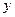 (см. указания к задаче Д-3.1) или применить теорему о движении центра масс системы (см. пример решения задачи №12).
(см. указания к задаче Д-3.1) или применить теорему о движении центра масс системы (см. пример решения задачи №12).


