Условия задач. Задача Д-2.0. Свободная материальная точка массы движется в горизонтальной плоскости по окружности радиуса под действием це
Задача Д-2.0. Свободная материальная точка 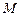 массы массы 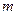 движется в горизонтальной плоскости по окружности радиуса движется в горизонтальной плоскости по окружности радиуса 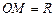 под действием центральной силы под действием центральной силы  с начальной скоростью с начальной скоростью 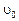 . .
Определить модуль силы 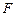 и её импульс за время, в течение которого точка переместится из положения и её импульс за время, в течение которого точка переместится из положения 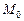 в положение в положение 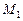 . Определить также ускорение точки в положении . Определить также ускорение точки в положении 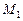 . .
Таблица Д-2.0
| № столбца
|
|
|
|
|
|
|
|
|
|
| | m, кг
|
| 1,5
| 2,4
| 1,8
| 0,6
| 0,8
| 2,4
| 1,5
| 1,6
| 1,8
| | R, м
| 0,8
| 1,4
| 1,5
| 1,6
| 0,8
| 1,2
| 0,8
| 0,6
| 0,8
| 0,5
| 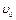 ,м/с ,м/с
| 1,8
| 1,6
| 2,2
| 2,8
| 2,6
| 3,0
| 1,5
| 2,5
| 2,0
| 3,0
| 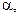 град. град.
|
|
|
|
|
|
|
|
|
|
| 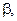 град. град.
|
|
|
|
|
|
|
|
|
|
|
Задача Д-2.1 Свободная материальная точка 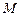 массы массы 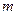 движется в горизонтальной плоскости по эллипсу с полуосями движется в горизонтальной плоскости по эллипсу с полуосями 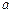 и и 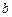 под действием центральной силы под действием центральной силы  с начальной скоростью с начальной скоростью 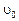 . .
Таблица Д-2.1
| № столбца
|
|
|
|
|
|
|
|
|
|
| | m, кг
| 0,6
| 0,8
| 1,2
| 1,6
| 2,0
| 2,4
| 1,5
| 2,5
| 2,6
| 1,8
| 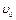 , м/с , м/с
| 0,9
| 1,2
| 1,6
| 1,8
| 1,5
| 1,0
| 2,0
| 1,8
| 1,2
| 1,5
| 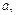 м м
| 0,4
| 0,6
| 0,8
| 1,0
| 0,3
| 0,5
| 1,2
| 1,4
| 0,2
| 0,7
| 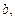 м м
| 0,2
| 0,4
| 0,6
| 0,8
| 0,1
| 0,3
| 0,8
| 1,0
| 0,1
| 0,4
| Определить скорость точки в положении 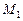 , импульс силы , импульс силы  за время, в течение которого точка переместится из положения за время, в течение которого точка переместится из положения 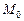 в положение в положение 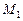 , и работу силы , и работу силы  на этом перемещении. на этом перемещении.
Задача Д-2.2. Тело 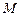 весом весом 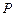 под действием силы тяжести скользит без трения по кольцу радиуса под действием силы тяжести скользит без трения по кольцу радиуса 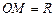 , расположенным в вертикальной плоскости. В начальный момент времени тело находилось в положении , расположенным в вертикальной плоскости. В начальный момент времени тело находилось в положении 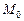 и имело скорость и имело скорость 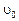 . .
Таблица Д-2.2
| № столбца
|
|
|
|
|
|
|
|
|
|
| 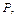 Н Н
|
|
|
|
|
|
|
|
|
|
| 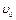 , м/с , м/с
| 2,6
| 0,3
| 4,0
| 5,0
| 5,2
| 4,4
| 4,8
| 5,0
| 3,4
| 8,0
| 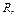 м м
| 0,2
| 0,4
| 0,6
| 0,8
| 1,0
| 0,5
| 0,7
| 0,5
| 0,3
| 1,2
| 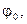 град. град.
|
|
|
|
|
|
|
|
|
|
| 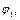 град. град.
|
|
|
|
|
|
|
|
|
|
| Считая тело материальной точкой, определить скорость и ускорение тела в положении 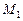 , а также импульс действующих сил за время перемещения тела из , а также импульс действующих сил за время перемещения тела из 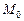 в в 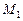 . .
Задача Д-2.3. Груз 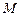 весом весом 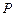 прикреплён к концу невесомого стержня длиной прикреплён к концу невесомого стержня длиной  , который может вращаться вокруг неподвижной оси , который может вращаться вокруг неподвижной оси  в вертикальной плоскости. В начальный момент времени стержень отклонили на угол в вертикальной плоскости. В начальный момент времени стержень отклонили на угол 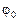 и сообщили грузу начальную скорость и сообщили грузу начальную скорость 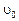 . .
Таблица Д-2.3
| № столбца
|
|
|
|
|
|
|
|
|
|
| 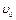 , м/с , м/с
|
| 5,6
| 6,4
| 6,0
| 5,8
| 8,2
| 4,4
| 6,8
| 8,6
| 4,8
| 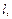 м м
| 0,2
| 0,6
| 0,6
| 0,4
| 0,3
| 0,5
| 0,15
| 0,25
| 0,2
| 0,1
| 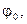 град. град.
|
|
|
|
|
|
|
|
|
|
| 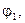 град. град.
|
|
|
|
|
|
|
|
|
|
| Определить скорость и ускорение груза, а также усилие в стержне в положении 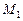 . Определить также импульс действующих на груз сил за время перемещения из положения . Определить также импульс действующих на груз сил за время перемещения из положения 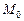 в положение в положение 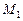 . .
Задача Д-2.4. На конце невесомого стержня длиной 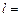 0,2 м закреплён груз 0,2 м закреплён груз 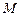 весом весом 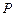 . В положении . В положении 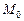 грузу сообщена начальная скорость грузу сообщена начальная скорость 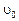 . .
Определить: 1. Скорость и ускорение груза в положении 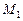 , определяемым углом , определяемым углом 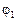 . 2. Продольную силу в стержне в этом положении. При вычислениях принять . 2. Продольную силу в стержне в этом положении. При вычислениях принять 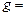 10 м/с2. 10 м/с2.
Таблица Д-2.4
| № столбца
|
|
|
|
|
|
|
|
|
|
| 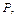 Н Н
|
|
|
|
|
|
|
|
|
|
| 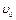 , м/с , м/с
| 2,1
| 2,2
| 2,5
| 2,4
| 2,3
| 2,6
| 2,8
| 3,0
| 2,7
| 2,5
| 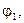 град. град.
|
|
|
|
|
|
|
|
|
|
|
Задача Д-2.5. Груз весом 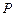 прикреплён к концу невесомого стержня длиной прикреплён к концу невесомого стержня длиной  и отклонён от вертикалина угол и отклонён от вертикалина угол 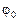 . В этом положении грузу сообщена начальная скорость . В этом положении грузу сообщена начальная скорость 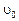 . .
Таблица Д-2.5
| № столбца
|
|
|
|
|
|
|
|
|
|
| 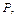 Н Н
|
|
|
|
|
|
|
|
|
|
| 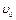 , м/с , м/с
| 0,8
| 1,5
| 2,8
| 1,8
| 3,6
| 1,6
| 2,4
| 1,4
| 1,0
| 3,0
| 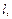 м м
| 0,1
| 0,3
| 0,5
| 0,8
| 1,0
| 0,6
| 0,4
| 0,5
| 0,2
| 0,9
| 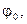 град. град.
|
|
|
|
| 22,5
|
|
|
|
| 22,5
| Определить: 1) наибольший угол 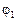 отклонения стержня от вертикали; 2) скорость и ускорение груза в положении отклонения стержня от вертикали; 2) скорость и ускорение груза в положении 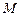 ; 3) импульс приложенных к грузу сил за время перемещения из положения ; 3) импульс приложенных к грузу сил за время перемещения из положения 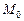 в положение в положение 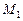 ; 4) продольную силу в стержне в положениях ; 4) продольную силу в стержне в положениях 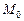 и и 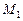 . .
Задача Д-2.6. Шарик весом 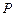 вложен в вертикально поставленный самострел, пружина которого сжата на вложен в вертикально поставленный самострел, пружина которого сжата на 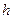 . Коэффициент жесткости пружины . Коэффициент жесткости пружины 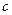 . .
Таблица Д-2.6
Определить, с какой скоростью вылетит шарик из самострела, и на какую высоту он поднимется при отсутствии сопротивления воздуха.
Задача Д-2.7. Шарик массой 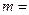 0,1кг выталкивается пружиной 0,1кг выталкивается пружиной 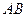 в трубку, расположенную в вертикальной плоскости и имеющей форму двух полуокружностей радиусами в трубку, расположенную в вертикальной плоскости и имеющей форму двух полуокружностей радиусами 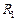 и и 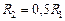 с центрами в точках с центрами в точках 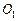 и и 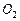 соответственно. Пружина в начальный момент времени сжата на величину соответственно. Пружина в начальный момент времени сжата на величину 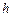 . Коэффициент жесткости пружины . Коэффициент жесткости пружины 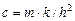 , где , где 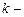 постоянная величина. Принимая шарик за материальную точку, определить скорость и ускорение шарика в положениях постоянная величина. Принимая шарик за материальную точку, определить скорость и ускорение шарика в положениях 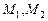 , а также силу давления шарика на стенку трубки в положении , а также силу давления шарика на стенку трубки в положении 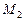 . Трением пренебречь. . Трением пренебречь.
Таблица Д-2.7
| № столбца
|
|
|
|
|
|
|
|
|
|
| 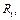 м м
| 0,5
| 0,2
| 0,1
| 0,3
| 0,4
| 0,6
| 0,5
| 0,3
| 0,1
| 0,7
| 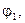 град. град.
|
|
|
|
|
|
|
|
|
|
| 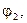 град. град.
|
|
|
|
|
|
|
|
|
|
| 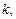 м2/с 2 м2/с 2
|
|
|
|
|
|
|
|
|
|
|
Задача Д-2.8. Вагонетка весом 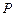 = 6 кН скатывается вниз с высоты = 6 кН скатывается вниз с высоты 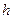 без начальной скорости по рельсам, расположенным по криволинейному пути и образующем затем круговое кольцо радиуса без начальной скорости по рельсам, расположенным по криволинейному пути и образующем затем круговое кольцо радиуса 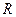 . .
Считая вагонетку материальной точкой, определить её скорость и ускорение, а также силу давления вагонетки на кольцо в тот момент, когда она находится в точке 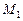 , положение которой определяется углом , положение которой определяется углом 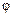 . Сопротивлением движению пренебречь. . Сопротивлением движению пренебречь.
Таблица Д-2.8
| № столбца
|
|
|
|
|
|
|
|
|
|
| 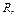 м м
|
|
| 1,5
|
| 2,5
|
|
|
|
|
| 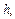 м м
|
|
|
|
|
|
|
|
|
|
| 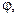 град. град.
|
|
|
|
|
|
|
|
|
|
|
Задача Д-2.9. Тело весом 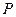 начинает движение в точке начинает движение в точке 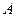 с начальной скоростью с начальной скоростью  по плоскости по плоскости 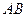 с углом наклона с углом наклона 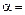 450, пройдя путь длиной 450, пройдя путь длиной  . Не меняя скорости в точке . Не меняя скорости в точке  , тело скользит по плоскости , тело скользит по плоскости  с углом наклона с углом наклона 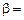 300, пройдя путь 300, пройдя путь 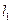 , а затем движется по горизонтальной плоскости , а затем движется по горизонтальной плоскости 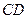 . Плоскости . Плоскости 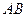 и и  гладкие. Коэффициент трения скольжения тела о плоскость на участке гладкие. Коэффициент трения скольжения тела о плоскость на участке 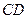 равен равен 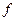 . Тело считать материальной точкой. . Тело считать материальной точкой.
Таблица Д-2.9
| № столбца
|
|
|
|
|
|
|
|
|
|
| 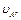 м/с м/с
| 4,5
|
|
|
|
|
|
|
|
|
| 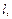 м м
| 1,2
| 0,8
| 1,6
| 1,5
| 1,8
| 1,0
| 2,4
| 2,6
| 1,8
| 2,0
| 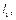 м м
| 0,8
| 0,5
| 0,8
| 1,0
| 4,0
| 2,0
| 1,6
| 1,3
| 1,2
| 1,6
| 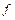
| 0,1
| 0,2
| 0,4
| 0,5
| 0,05
| 0,1
| 0,08
| 0,1
| 0,06
| 0,1
| Определить пройденный телом путь 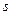 на участке на участке 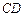 до остановки в точке до остановки в точке 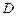 , а также общее время движения. , а также общее время движения.
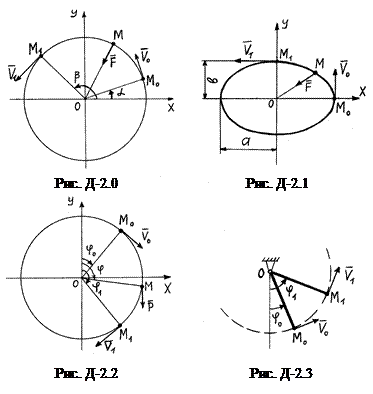
Схемы к задачам Д- 2
Указания к решению задач Д- 2
Задача Д-2.0. Применяя теорему об изменении момента количества движения точки относительно оси 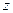 , докажите, что при действии центральной силы точка совершает равномерное движение. Тогда ускорение точки , докажите, что при действии центральной силы точка совершает равномерное движение. Тогда ускорение точки 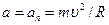 , где , где 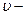 её скорость. её скорость.
Модуль силы 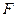 можно найти, применяя второй закон динамики точки в проекции на главную нормаль: можно найти, применяя второй закон динамики точки в проекции на главную нормаль: 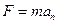 . Для определения импульса силы рекомендуется применить теорему об изменении количества движении точки в проекциях на оси . Для определения импульса силы рекомендуется применить теорему об изменении количества движении точки в проекциях на оси  , причём модуль импульса силы найти по формуле , причём модуль импульса силы найти по формуле 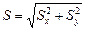 , где , где 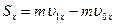 , , 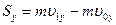 . .
Задача Д-2.1. Для определения скорости 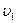 следует применить теорему об изменении момента количества движения точки относительно оси следует применить теорему об изменении момента количества движения точки относительно оси 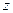 , учитывая, что , учитывая, что 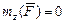 . Для определения импульса силы применить теорему об изменении количества движения точки в проекциях на оси . Для определения импульса силы применить теорему об изменении количества движения точки в проекциях на оси  , а для определения работы силы , а для определения работы силы 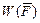 применить теорему об изменении кинетической энергии точки на перемещении применить теорему об изменении кинетической энергии точки на перемещении 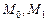 : : 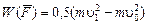 . .
Задачи Д-2.2–Д-2.5. Для определения скорости точки в положении 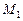 следует применить теорему об изменении кинетической энергии точки на перемещении следует применить теорему об изменении кинетической энергии точки на перемещении 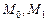 . Ускорение точки . Ускорение точки 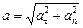 . Для определения касательного ускорения . Для определения касательного ускорения 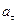 применить теорему об изменении момента количества движения точки относительно точки применить теорему об изменении момента количества движения точки относительно точки  : : 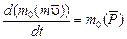 или или 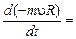 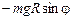 . Отсюда, сокращая на . Отсюда, сокращая на 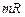 , получим , получим 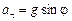 . Обратите внимание на знаки моментов силы тяжести и количества движения точки. Если угол . Обратите внимание на знаки моментов силы тяжести и количества движения точки. Если угол 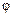 отсчитывается против хода часовой стрелки, то отсчитывается против хода часовой стрелки, то 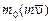 >0. В задаче Д-2.2 угол >0. В задаче Д-2.2 угол 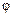 отсчитывается по часовой стрелке, поэтому отсчитывается по часовой стрелке, поэтому 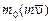 <0. Нормальное ускорение <0. Нормальное ускорение 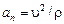 , где , где 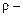 радиус траектории. В случае, если траекторией является окружность радиуса радиус траектории. В случае, если траекторией является окружность радиуса 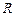 , то , то 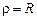 . .
Продольную силу в стержне можно найти, решая первую задачу динамики: 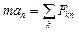 , нормальное ускорение , нормальное ускорение 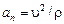 . Модуль импульса силы найти как в задаче Д-2.0. . Модуль импульса силы найти как в задаче Д-2.0.
Задача Д-2.6. Движение шарика на участке 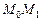 происходит под действием силы тяжести и силы упругости, а на участке происходит под действием силы тяжести и силы упругости, а на участке 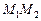 – только под действием силы тяжести. Применяя на обоих участках теорему об изменении кинетической энергии точки, можно найти высоту подъёма – только под действием силы тяжести. Применяя на обоих участках теорему об изменении кинетической энергии точки, можно найти высоту подъёма 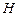 . Обратите внимание на единицы измерений . Обратите внимание на единицы измерений 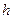 и и 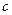 . .
Задача Д-2.7. Сначала рекомендуется рассмотреть движение шарика на участке 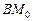 , которое происходит под действием силы упругости пружины, и определить скорость шарика в положении , которое происходит под действием силы упругости пружины, и определить скорость шарика в положении 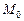 . Затем, применяя на участках . Затем, применяя на участках 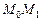 и и 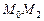 теорему об изменении кинетической энергии, можно найти скорости шарика в положениях теорему об изменении кинетической энергии, можно найти скорости шарика в положениях 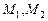 . Давление шарика на стенку трубки определяется решением первой задачи динамики: . Давление шарика на стенку трубки определяется решением первой задачи динамики: 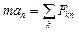 . .
Задача Д-2.8. Для определения скоростей точки в положениях 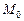 , , 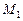 рекомендуется применить теорему об изменении кинетической энергии на участках рекомендуется применить теорему об изменении кинетической энергии на участках 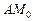 и и 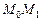 . Ускорение вагонетки определяется так же, как и в задачах Д-2.2–Д-2.5. . Ускорение вагонетки определяется так же, как и в задачах Д-2.2–Д-2.5.
Задача Д-2.9. При решении этой задачи рекомендуется применить теорему об изменении кинетической энергии и теорему об изменении количества движения точки последовательно на участках 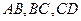 . Очевидно, что в момент остановки скорость тела равна нулю. . Очевидно, что в момент остановки скорость тела равна нулю.

Важнейшие способы обработки и анализа рядов динамики Не во всех случаях эмпирические данные рядов динамики позволяют определить тенденцию изменения явления во времени...
|

ТЕОРЕТИЧЕСКАЯ МЕХАНИКА Статика является частью теоретической механики, изучающей условия, при которых тело находится под действием заданной системы сил...
|

Теория усилителей. Схема Основная масса современных аналоговых и аналого-цифровых электронных устройств выполняется на специализированных микросхемах...
|

Логические цифровые микросхемы Более сложные элементы цифровой схемотехники (триггеры, мультиплексоры, декодеры и т.д.) не имеют...
|
Признаки классификации безопасности Можно выделить следующие признаки классификации безопасности.
1. По признаку масштабности принято различать следующие относительно самостоятельные геополитические уровни и виды безопасности.
1.1. Международная безопасность (глобальная и...
Прием и регистрация больных Пути госпитализации больных в стационар могут быть различны. В центральное приемное отделение больные могут быть доставлены:
1) машиной скорой медицинской помощи в случае возникновения острого или обострения хронического заболевания...
ПУНКЦИЯ И КАТЕТЕРИЗАЦИЯ ПОДКЛЮЧИЧНОЙ ВЕНЫ
Пункцию и катетеризацию подключичной вены обычно производит хирург или анестезиолог, иногда — специально обученный терапевт...
|
КОНСТРУКЦИЯ КОЛЕСНОЙ ПАРЫ ВАГОНА Тип колёсной пары определяется типом оси и диаметром колес. Согласно ГОСТ 4835-2006* устанавливаются типы колесных пар для грузовых вагонов с осями РУ1Ш и РВ2Ш и колесами диаметром по кругу катания 957 мм. Номинальный диаметр колеса – 950 мм...
Философские школы эпохи эллинизма (неоплатонизм, эпикуреизм, стоицизм, скептицизм). Эпоха эллинизма со времени походов Александра Македонского, в результате которых была образована гигантская империя от Индии на востоке до Греции и Македонии на западе...
Демографияда "Демографиялық жарылыс" дегеніміз не? Демография (грекше демос — халық) — халықтың құрылымын...
|
|

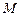 массы
массы 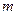 движется в горизонтальной плоскости по окружности радиуса
движется в горизонтальной плоскости по окружности радиуса 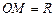 под действием центральной силы
под действием центральной силы  с начальной скоростью
с начальной скоростью 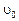 .
.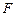 и её импульс за время, в течение которого точка переместится из положения
и её импульс за время, в течение которого точка переместится из положения 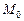 в положение
в положение 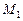 . Определить также ускорение точки в положении
. Определить также ускорение точки в положении 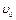 ,м/с
,м/с
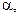 град.
град.
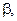 град.
град.
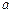 и
и 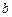 под действием центральной силы
под действием центральной силы 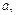 м
м
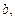 м
м
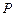 под действием силы тяжести скользит без трения по кольцу радиуса
под действием силы тяжести скользит без трения по кольцу радиуса 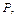 Н
Н
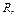 м
м
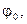 град.
град.
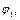 град.
град.
 , который может вращаться вокруг неподвижной оси
, который может вращаться вокруг неподвижной оси  в вертикальной плоскости. В начальный момент времени стержень отклонили на угол
в вертикальной плоскости. В начальный момент времени стержень отклонили на угол 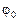 и сообщили грузу начальную скорость
и сообщили грузу начальную скорость 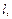 м
м
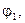 град.
град.
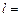 0,2 м закреплён груз
0,2 м закреплён груз 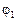 . 2. Продольную силу в стержне в этом положении. При вычислениях принять
. 2. Продольную силу в стержне в этом положении. При вычислениях принять 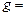 10 м/с2.
10 м/с2.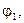 град.
град.
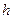 . Коэффициент жесткости пружины
. Коэффициент жесткости пружины 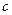 .
.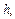 см
см
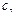 Н/см,
Н/см,
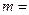 0,1кг выталкивается пружиной
0,1кг выталкивается пружиной 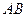 в трубку, расположенную в вертикальной плоскости и имеющей форму двух полуокружностей радиусами
в трубку, расположенную в вертикальной плоскости и имеющей форму двух полуокружностей радиусами 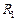 и
и 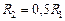 с центрами в точках
с центрами в точках 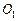 и
и 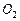 соответственно. Пружина в начальный момент времени сжата на величину
соответственно. Пружина в начальный момент времени сжата на величину 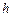 . Коэффициент жесткости пружины
. Коэффициент жесткости пружины 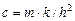 , где
, где 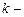 постоянная величина. Принимая шарик за материальную точку, определить скорость и ускорение шарика в положениях
постоянная величина. Принимая шарик за материальную точку, определить скорость и ускорение шарика в положениях 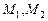 , а также силу давления шарика на стенку трубки в положении
, а также силу давления шарика на стенку трубки в положении 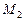 . Трением пренебречь.
. Трением пренебречь.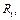 м
м
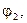 град.
град.
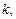 м2/с 2
м2/с 2
 .
. . Сопротивлением движению пренебречь.
. Сопротивлением движению пренебречь.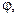 град.
град.
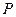 начинает движение в точке
начинает движение в точке 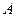 с начальной скоростью
с начальной скоростью  по плоскости
по плоскости 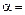 450, пройдя путь длиной
450, пройдя путь длиной  , тело скользит по плоскости
, тело скользит по плоскости  с углом наклона
с углом наклона 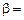 300, пройдя путь
300, пройдя путь 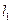 , а затем движется по горизонтальной плоскости
, а затем движется по горизонтальной плоскости 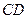 . Плоскости
. Плоскости 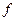 . Тело считать материальной точкой.
. Тело считать материальной точкой.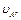 м/с
м/с
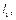 м
м
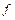
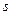 на участке
на участке 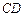 до остановки в точке
до остановки в точке 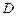 , а также общее время движения.
, а также общее время движения.

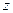 , докажите, что при действии центральной силы точка совершает равномерное движение. Тогда ускорение точки
, докажите, что при действии центральной силы точка совершает равномерное движение. Тогда ускорение точки 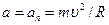 , где
, где 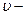 её скорость.
её скорость.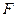 можно найти, применяя второй закон динамики точки в проекции на главную нормаль:
можно найти, применяя второй закон динамики точки в проекции на главную нормаль: 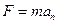 . Для определения импульса силы рекомендуется применить теорему об изменении количества движении точки в проекциях на оси
. Для определения импульса силы рекомендуется применить теорему об изменении количества движении точки в проекциях на оси  , причём модуль импульса силы найти по формуле
, причём модуль импульса силы найти по формуле 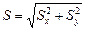 , где
, где 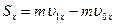 ,
, 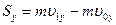 .
.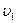 следует применить теорему об изменении момента количества движения точки относительно оси
следует применить теорему об изменении момента количества движения точки относительно оси 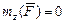 . Для определения импульса силы применить теорему об изменении количества движения точки в проекциях на оси
. Для определения импульса силы применить теорему об изменении количества движения точки в проекциях на оси 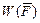 применить теорему об изменении кинетической энергии точки на перемещении
применить теорему об изменении кинетической энергии точки на перемещении 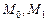 :
: 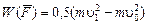 .
.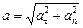 . Для определения касательного ускорения
. Для определения касательного ускорения 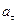 применить теорему об изменении момента количества движения точки относительно точки
применить теорему об изменении момента количества движения точки относительно точки 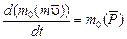 или
или 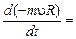
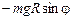 . Отсюда, сокращая на
. Отсюда, сокращая на 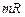 , получим
, получим 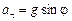 . Обратите внимание на знаки моментов силы тяжести и количества движения точки. Если угол
. Обратите внимание на знаки моментов силы тяжести и количества движения точки. Если угол 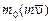 >0. В задаче Д-2.2 угол
>0. В задаче Д-2.2 угол 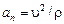 , где
, где 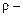 радиус траектории. В случае, если траекторией является окружность радиуса
радиус траектории. В случае, если траекторией является окружность радиуса 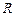 , то
, то 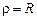 .
.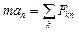 , нормальное ускорение
, нормальное ускорение 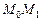 происходит под действием силы тяжести и силы упругости, а на участке
происходит под действием силы тяжести и силы упругости, а на участке 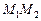 – только под действием силы тяжести. Применяя на обоих участках теорему об изменении кинетической энергии точки, можно найти высоту подъёма
– только под действием силы тяжести. Применяя на обоих участках теорему об изменении кинетической энергии точки, можно найти высоту подъёма 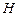 . Обратите внимание на единицы измерений
. Обратите внимание на единицы измерений 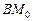 , которое происходит под действием силы упругости пружины, и определить скорость шарика в положении
, которое происходит под действием силы упругости пружины, и определить скорость шарика в положении 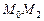 теорему об изменении кинетической энергии, можно найти скорости шарика в положениях
теорему об изменении кинетической энергии, можно найти скорости шарика в положениях 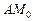 и
и  . Очевидно, что в момент остановки скорость тела равна нулю.
. Очевидно, что в момент остановки скорость тела равна нулю.


