Точка движется в плоскости 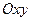 по закону:
по закону: 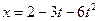 (см),
(см),  (см). Найти уравнение траектории. В момент времени
(см). Найти уравнение траектории. В момент времени 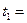 1с определить скорость точки, ускорение и их составляющие на координатные и естественные оси, а также радиус кривизны траектории для соответствующего момента времени.
1с определить скорость точки, ускорение и их составляющие на координатные и естественные оси, а также радиус кривизны траектории для соответствующего момента времени.
Решение.
1) Найдём уравнение траектории.
Для этого из уравнений движения исключаем параметр 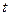 . Второе уравнение запишем в виде
. Второе уравнение запишем в виде  и найдём разность
и найдём разность 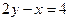 . Это и есть уравнение траектории (уравнение прямой). Следовательно, движение точки прямолинейное. Так как время изменяется в интервале
. Это и есть уравнение траектории (уравнение прямой). Следовательно, движение точки прямолинейное. Так как время изменяется в интервале 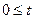 < ∞, то координаты точки изменяются в интервалах 2 см
< ∞, то координаты точки изменяются в интервалах 2 см 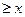 > – ∞, 3 см
> – ∞, 3 см 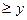 > – ∞. Начальное положение точки при
> – ∞. Начальное положение точки при 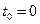 определяется координатами
определяется координатами  = 2 см;
= 2 см;  = 3 см;
= 3 см; 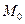 (2;3). Для момента времени
(2;3). Для момента времени 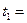 1с
1с  2 − 3 − 6 = − 7 см;
2 − 3 − 6 = − 7 см;  3 − 1,5 − 3 =
3 − 1,5 − 3 =
= 1,5 см; 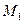 (–7;–1,5). Прямую строим по двум точкам:
(–7;–1,5). Прямую строим по двум точкам: 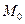 и
и 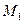 (рис.8).
(рис.8).
2) Определим скорость точки.
Сначала найдём проекции скорости на оси  :
:
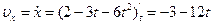 ;
;
 .
.
В момент времени 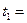 1с:
1с: 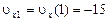 см/с,
см/с, 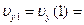 = –7,5 см/с. Модуль скорости
= –7,5 см/с. Модуль скорости 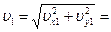 16,77 см/с.
16,77 см/с.
На рис.8 от точки
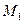
проведём оси
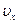
,
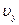
и на них отложим
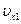
,
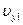
, по которым построим вектор скорости, направленный по касательной к траектории. В случае прямолинейного движения точки вектор скорости направлен вдоль траектории.
3) Определим ускорение точки.
Проекции ускорения на оси  :
:
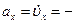 12 см/с2,
12 см/с2, 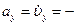 6 см/с2.
6 см/с2.
Модуль ускорения точки 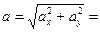 13,42 см/с2.
13,42 см/с2.
На рис.6 от точки 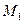 проведём оси
проведём оси 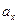 ,
, 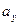 и отложим на них
и отложим на них  ,
,  . Вектор ускорения
. Вектор ускорения 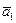 построим по составляющим
построим по составляющим 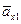 ,
, 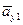 .
.
Обратим внимание, что единицы измерений координат  , проекций скорости
, проекций скорости 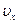 ,
, 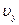 и ускорения
и ускорения 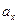 ,
, 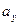 отличаются. Поэтому при построении траектории, векторов скорости и ускорения могут быть назначены разные единицы масштаба.
отличаются. Поэтому при построении траектории, векторов скорости и ускорения могут быть назначены разные единицы масштаба.
4) Определим составляющие ускорения на касательную и главную нормаль. Найдём радиус кривизны траектории.
Направим вдоль вектора скорости касательную, а перпендикулярно касательной – главную нормаль. На эти оси спроектируем конец вектора ускорения. Таким образом, вектор ускорения раскладывается на касательную и нормальную составляющие: 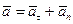 , а модуль ускорения равен
, а модуль ускорения равен 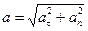 .
.
Касательное ускорение вычисляется по формуле:
 . Тогда можно определить нормальное ускорение
. Тогда можно определить нормальное ускорение 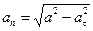 . Радиус кривизны траектории
. Радиус кривизны траектории 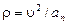 .
.
В случае прямолинейного движения точки 
 и, следовательно,
и, следовательно, 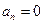 ,
, 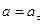 . Радиус кривизны траектории
. Радиус кривизны траектории  .
.
Ответ: уравнение траектории: 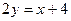 ;
;  15 см/с,
15 см/с, 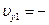 7,5 см/с,
7,5 см/с,  16,77 см/с;
16,77 см/с; 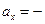 12 см/с2,
12 см/с2, 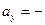 6 см/с2,
6 см/с2, 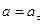 =13,42 см/с2,
=13,42 см/с2, 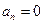 ;
;  . Поскольку
. Поскольку  > 0, то движение точки будет ускоренным – на рисунке векторы скорости и касательного ускорения имеют одинаковые направления. Касательное ускорение точки постоянное (не зависит от времени), следовательно, движение точки будет равноускоренным.
> 0, то движение точки будет ускоренным – на рисунке векторы скорости и касательного ускорения имеют одинаковые направления. Касательное ускорение точки постоянное (не зависит от времени), следовательно, движение точки будет равноускоренным.
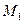 проведём оси
проведём оси 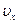 ,
, 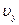 и на них отложим
и на них отложим 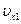 ,
, 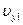 , по которым построим вектор скорости, направленный по касательной к траектории. В случае прямолинейного движения точки вектор скорости направлен вдоль траектории.
, по которым построим вектор скорости, направленный по касательной к траектории. В случае прямолинейного движения точки вектор скорости направлен вдоль траектории.

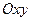 по закону:
по закону: 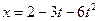 (см),
(см),  (см). Найти уравнение траектории. В момент времени
(см). Найти уравнение траектории. В момент времени 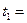 1с определить скорость точки, ускорение и их составляющие на координатные и естественные оси, а также радиус кривизны траектории для соответствующего момента времени.
1с определить скорость точки, ускорение и их составляющие на координатные и естественные оси, а также радиус кривизны траектории для соответствующего момента времени.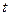 . Второе уравнение запишем в виде
. Второе уравнение запишем в виде  и найдём разность
и найдём разность 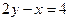 . Это и есть уравнение траектории (уравнение прямой). Следовательно, движение точки прямолинейное. Так как время изменяется в интервале
. Это и есть уравнение траектории (уравнение прямой). Следовательно, движение точки прямолинейное. Так как время изменяется в интервале 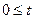 < ∞, то координаты точки изменяются в интервалах 2 см
< ∞, то координаты точки изменяются в интервалах 2 см 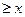 > – ∞, 3 см
> – ∞, 3 см 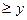 > – ∞. Начальное положение точки при
> – ∞. Начальное положение точки при 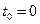 определяется координатами
определяется координатами  = 2 см;
= 2 см;  = 3 см;
= 3 см; 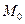 (2;3). Для момента времени
(2;3). Для момента времени  2 − 3 − 6 = − 7 см;
2 − 3 − 6 = − 7 см;  3 − 1,5 − 3 =
3 − 1,5 − 3 = :
: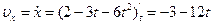 ;
; .
.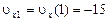 см/с,
см/с, 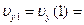 = –7,5 см/с. Модуль скорости
= –7,5 см/с. Модуль скорости 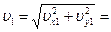 16,77 см/с.
16,77 см/с.
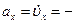 12 см/с2,
12 см/с2, 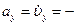 6 см/с2.
6 см/с2.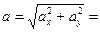 13,42 см/с2.
13,42 см/с2.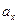 ,
, 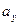 и отложим на них
и отложим на них  ,
,  . Вектор ускорения
. Вектор ускорения 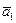 построим по составляющим
построим по составляющим 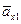 ,
, 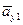 .
.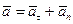 , а модуль ускорения равен
, а модуль ускорения равен 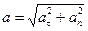 .
. . Тогда можно определить нормальное ускорение
. Тогда можно определить нормальное ускорение 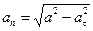 . Радиус кривизны траектории
. Радиус кривизны траектории 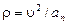 .
.
 и, следовательно,
и, следовательно, 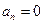 ,
, 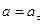 . Радиус кривизны траектории
. Радиус кривизны траектории  .
.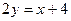 ;
;  15 см/с,
15 см/с, 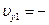 7,5 см/с,
7,5 см/с,  16,77 см/с;
16,77 см/с; 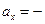 12 см/с2,
12 см/с2, 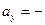 6 см/с2,
6 см/с2,  > 0, то движение точки будет ускоренным – на рисунке векторы скорости и касательного ускорения имеют одинаковые направления. Касательное ускорение точки постоянное (не зависит от времени), следовательно, движение точки будет равноускоренным.
> 0, то движение точки будет ускоренным – на рисунке векторы скорости и касательного ускорения имеют одинаковые направления. Касательное ускорение точки постоянное (не зависит от времени), следовательно, движение точки будет равноускоренным.


