Тело  весом
весом  18 Н скользит без трения под действием силы тяжести по кольцу радиуса
18 Н скользит без трения под действием силы тяжести по кольцу радиуса 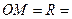 0,45 м, расположенным в вертикальной плоскости (рис.14). В начальный момент времени тело находится в положении
0,45 м, расположенным в вертикальной плоскости (рис.14). В начальный момент времени тело находится в положении 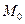 (
(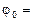 60о) и имеет скорость
60о) и имеет скорость 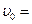 6 м/с.
6 м/с.
Считая тело  материальной точкой, определить:
материальной точкой, определить:
1) скорость и ускорение тела в положении 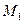 (
(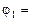 225о);
225о);
2) импульс действующих сил за время перемещения тела из положения 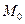 в положение
в положение 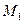 .
.
Решение. На тело действуют сила тяжести
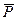
и нормальная реакция кольца
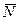
. Определим скорость
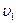
тела в положении
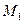
. Применим теорему об изменении кинетической энергии материальной точки:
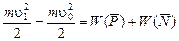 . Работа силы
. Работа силы 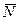 на перемещении
на перемещении 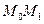 равна нулю, работа силы тяжести
равна нулю, работа силы тяжести  . Масса тела
. Масса тела 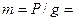 18 / 10 = 1,8 кг. Вертикальное перемещение тела
18 / 10 = 1,8 кг. Вертикальное перемещение тела 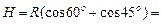 0,45 м(0,5 + 0,707) = 0,543 м. Тогда получим 1,8 (
0,45 м(0,5 + 0,707) = 0,543 м. Тогда получим 1,8 (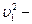 36) /2 = 18∙0,543. Отсюда находим скорость тела в положении
36) /2 = 18∙0,543. Отсюда находим скорость тела в положении 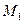 :
:  6,85 м/с.
6,85 м/с.
Определим ускорение тела в положении 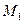 . Оно состоит из суммы векторов касательного и нормального ускорений:
. Оно состоит из суммы векторов касательного и нормального ускорений: 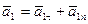 . Модуль нормального ускорения определяется по формуле
. Модуль нормального ускорения определяется по формуле 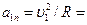 (6,85 м/с) 2 / 0,45 м = 104 м/с2. Вектор нормального ускорения направлен к центру кольца. Для определения касательного ускорения применим теорему об изменении момента количества движения точки
(6,85 м/с) 2 / 0,45 м = 104 м/с2. Вектор нормального ускорения направлен к центру кольца. Для определения касательного ускорения применим теорему об изменении момента количества движения точки  относительно центра
относительно центра  в алгебраической форме:
в алгебраической форме:
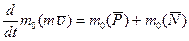 .
.
Момент количества движения точки 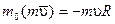 ; момент силы тяжести
; момент силы тяжести 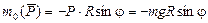 ; момент нормальной ре-акции
; момент нормальной ре-акции 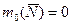 , т.к. линия действия силы
, т.к. линия действия силы  пересекает точку
пересекает точку  . Тогда
. Тогда 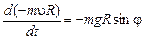 . Отсюда получим величину касательного ускорения
. Отсюда получим величину касательного ускорения 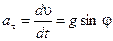 . Определим касательное ускорение в точке
. Определим касательное ускорение в точке 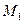 :
: 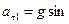 225о = 10 м/с2∙(–0,707) = –7,07 м/с2.
225о = 10 м/с2∙(–0,707) = –7,07 м/с2.
Обратим внимание, что в интервале 0<  <180о тело движется ускоренно (
<180о тело движется ускоренно ( > 0), а в интервале 180о<
> 0), а в интервале 180о< 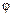 <360о тело движется замедленно (
<360о тело движется замедленно ( < 0). Модуль ускорения точки в положении
< 0). Модуль ускорения точки в положении 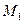 :
:
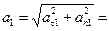
 м/с2.
м/с2.
Определим импульс действующих на тело сил за время перемещения его из положения 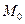 в положение
в положение 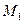 . Для этого воспользуемся теоремой об изменении количества движения точки:
. Для этого воспользуемся теоремой об изменении количества движения точки:
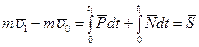 , (1)
, (1)
где 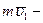 вектор количества движения тела в положении
вектор количества движения тела в положении 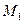 ;
;
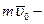 вектор количества движения тела в положении
вектор количества движения тела в положении 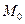 ;
;
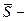 вектор импульса сил за время
вектор импульса сил за время 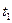 движения тела по кольцу из точки
движения тела по кольцу из точки 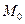 в точку
в точку 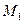 .
.
Проектируем векторное уравнение (1) на оси  (см. рис.14):
(см. рис.14):
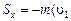 cos45o
cos45o 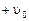 cos60o) = – 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с∙ 0,5) =
cos60o) = – 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с∙ 0,5) =
= – 14,1 Н∙с – проекция вектора импульса сил на ось x;
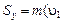 sin45o–(–
sin45o–(– 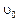 sin60o)) = 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с ∙ 0,866) =
sin60o)) = 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с ∙ 0,866) =
= 18,1 Н∙с – проекция вектора импульса сил на ось y.
Модуль импульса сил: 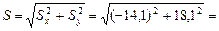 22,9 Н∙с.
22,9 Н∙с.
Ответ:  6,85 м/с;
6,85 м/с;  104,2 м/с2;
104,2 м/с2;  22,9 Н∙с.
22,9 Н∙с.
 и нормальная реакция кольца
и нормальная реакция кольца 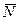 . Определим скорость
. Определим скорость 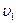 тела в положении
тела в положении 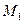 . Применим теорему об изменении кинетической энергии материальной точки:
. Применим теорему об изменении кинетической энергии материальной точки:

 весом
весом  18 Н скользит без трения под действием силы тяжести по кольцу радиуса
18 Н скользит без трения под действием силы тяжести по кольцу радиуса 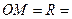 0,45 м, расположенным в вертикальной плоскости (рис.14). В начальный момент времени тело находится в положении
0,45 м, расположенным в вертикальной плоскости (рис.14). В начальный момент времени тело находится в положении 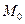 (
(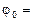 60о) и имеет скорость
60о) и имеет скорость 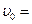 6 м/с.
6 м/с.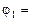 225о);
225о);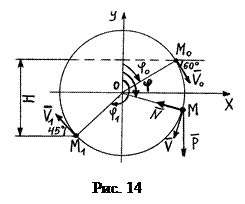
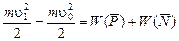 . Работа силы
. Работа силы  равна нулю, работа силы тяжести
равна нулю, работа силы тяжести  . Масса тела
. Масса тела 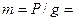 18 / 10 = 1,8 кг. Вертикальное перемещение тела
18 / 10 = 1,8 кг. Вертикальное перемещение тела 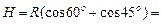 0,45 м(0,5 + 0,707) = 0,543 м. Тогда получим 1,8 (
0,45 м(0,5 + 0,707) = 0,543 м. Тогда получим 1,8 (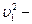 36) /2 = 18∙0,543. Отсюда находим скорость тела в положении
36) /2 = 18∙0,543. Отсюда находим скорость тела в положении  6,85 м/с.
6,85 м/с.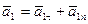 . Модуль нормального ускорения определяется по формуле
. Модуль нормального ускорения определяется по формуле 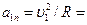 (6,85 м/с) 2 / 0,45 м = 104 м/с2. Вектор нормального ускорения направлен к центру кольца. Для определения касательного ускорения применим теорему об изменении момента количества движения точки
(6,85 м/с) 2 / 0,45 м = 104 м/с2. Вектор нормального ускорения направлен к центру кольца. Для определения касательного ускорения применим теорему об изменении момента количества движения точки  в алгебраической форме:
в алгебраической форме: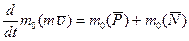 .
.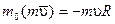 ; момент силы тяжести
; момент силы тяжести 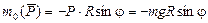 ; момент нормальной ре-акции
; момент нормальной ре-акции 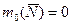 , т.к. линия действия силы
, т.к. линия действия силы 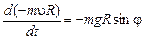 . Отсюда получим величину касательного ускорения
. Отсюда получим величину касательного ускорения 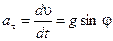 . Определим касательное ускорение в точке
. Определим касательное ускорение в точке 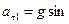 225о = 10 м/с2∙(–0,707) = –7,07 м/с2.
225о = 10 м/с2∙(–0,707) = –7,07 м/с2.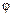 <180о тело движется ускоренно (
<180о тело движется ускоренно ( > 0), а в интервале 180о<
> 0), а в интервале 180о< 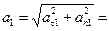
 м/с2.
м/с2.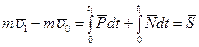 , (1)
, (1)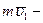 вектор количества движения тела в положении
вектор количества движения тела в положении 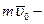 вектор количества движения тела в положении
вектор количества движения тела в положении 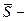 вектор импульса сил за время
вектор импульса сил за время 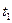 движения тела по кольцу из точки
движения тела по кольцу из точки  (см. рис.14):
(см. рис.14):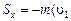 cos45o
cos45o 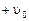 cos60o) = – 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с∙ 0,5) =
cos60o) = – 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с∙ 0,5) =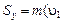 sin45o–(–
sin45o–(– 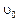 sin60o)) = 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с ∙ 0,866) =
sin60o)) = 1,8 кг(6,85 м/с∙ 0,707 + 6 м/с ∙ 0,866) =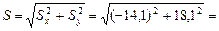 22,9 Н∙с.
22,9 Н∙с. 104,2 м/с2;
104,2 м/с2;  22,9 Н∙с.
22,9 Н∙с.


