 Однородный цилиндрический барабан весом
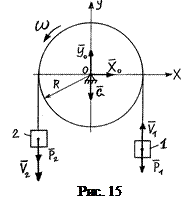
Однородный цилиндрический барабан весом 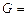 150Н и радиусом
150Н и радиусом  0,3 м вращается вокруг горизонтальной оси
0,3 м вращается вокруг горизонтальной оси  под действием двух грузов весами
под действием двух грузов весами  1600Н и
1600Н и  1200Н, подвешенных на концах каната, навёрнутого на барабан (рис.15). Пренебрегая весом каната, определить силу давления барабана на неподвижную ось
1200Н, подвешенных на концах каната, навёрнутого на барабан (рис.15). Пренебрегая весом каната, определить силу давления барабана на неподвижную ось  .
.
Решение. Сила давления на ось барабана численно равна реакции опоры  , которую разложим на составляющие
, которую разложим на составляющие  . Из уравнения
. Из уравнения  следует, что
следует, что  .
.
Реакцию  определим в два этапа. Сначала с помощью теоремы об изменения момента количества движения механической системы относительно точки
определим в два этапа. Сначала с помощью теоремы об изменения момента количества движения механической системы относительно точки  в алгебраической форме
в алгебраической форме
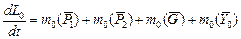
найдём ускорение движущихся грузов. Моменты сил 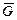 и
и  относительно точки
относительно точки  равны нулю, т.к. точка
равны нулю, т.к. точка  лежит на линиях действия этих сил. Моменты сил
лежит на линиях действия этих сил. Моменты сил 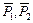 :
:  ,
,  . Следовательно,
. Следовательно,  Н∙м.
Н∙м.
Найдём кинетический момент механической системы относительно точки  , который складывается из кинетических моментов барабана
, который складывается из кинетических моментов барабана  , груза 1
, груза 1 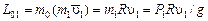 и груза 2
и груза 2  . Заметим, что скорости грузов одинаковы
. Заметим, что скорости грузов одинаковы  , а угловая скорость барабана
, а угловая скорость барабана 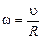 . Момент инерции барабана
. Момент инерции барабана  . Тогда получим
. Тогда получим

 .
.
Производная по времени 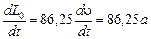 . Но выше было определено
. Но выше было определено  Н∙м. Тогда ускорение грузов
Н∙м. Тогда ускорение грузов  м/с2.
м/с2.
Ускорение получилось постоянным и отрицательным. Следовательно, барабан вращается равноускоренно по часовой стрелке. Это согласуется с условием задачи: 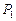 >
> 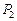 .
.
На втором этапе решения задачи определим реакцию  . Теорема об изменении главного вектора количества движения механической системы в проекции на ось
. Теорема об изменении главного вектора количества движения механической системы в проекции на ось  имеет вид:
имеет вид:


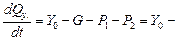 2950 Н. (2)
2950 Н. (2)
Вектор количества движения системы складывается из векторов количества движений барабана и грузов: 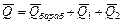 .
.
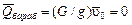 , т.к. скорость центра масс барабана
, т.к. скорость центра масс барабана  ;
;
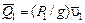 ;
;  . Проекция главного вектора количества движения системы на ось
. Проекция главного вектора количества движения системы на ось  :
: 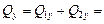
 .
.
Берём производную  = 40∙(–1,39) = –55,6 Н.
= 40∙(–1,39) = –55,6 Н.
Из (2) найдём  Н= – 55,6 Н+ 2950 Н= 2894,4 Н.
Н= – 55,6 Н+ 2950 Н= 2894,4 Н.
Ответ: сила давления барабана на ось равна 2,89 кН.

 Однородный цилиндрический барабан весом
Однородный цилиндрический барабан весом 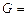 150Н и радиусом
150Н и радиусом  0,3 м вращается вокруг горизонтальной оси
0,3 м вращается вокруг горизонтальной оси  под действием двух грузов весами
под действием двух грузов весами  1600Н и
1600Н и  1200Н, подвешенных на концах каната, навёрнутого на барабан (рис.15). Пренебрегая весом каната, определить силу давления барабана на неподвижную ось
1200Н, подвешенных на концах каната, навёрнутого на барабан (рис.15). Пренебрегая весом каната, определить силу давления барабана на неподвижную ось  , которую разложим на составляющие
, которую разложим на составляющие  . Из уравнения
. Из уравнения  следует, что
следует, что  .
. определим в два этапа. Сначала с помощью теоремы об изменения момента количества движения механической системы относительно точки
определим в два этапа. Сначала с помощью теоремы об изменения момента количества движения механической системы относительно точки 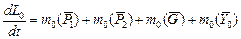
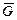 и
и  относительно точки
относительно точки 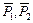 :
:  ,
,  . Следовательно,
. Следовательно,  Н∙м.
Н∙м. , груза 1
, груза 1 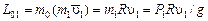 и груза 2
и груза 2  . Заметим, что скорости грузов одинаковы
. Заметим, что скорости грузов одинаковы  , а угловая скорость барабана
, а угловая скорость барабана 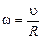 . Момент инерции барабана
. Момент инерции барабана  . Тогда получим
. Тогда получим
 .
.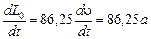 . Но выше было определено
. Но выше было определено  Н∙м. Тогда ускорение грузов
Н∙м. Тогда ускорение грузов  м/с2.
м/с2.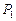 >
> 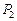 .
. имеет вид:
имеет вид:

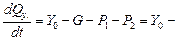 2950 Н. (2)
2950 Н. (2)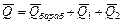 .
.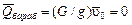 , т.к. скорость центра масс барабана
, т.к. скорость центра масс барабана  ;
;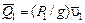 ;
;  . Проекция главного вектора количества движения системы на ось
. Проекция главного вектора количества движения системы на ось 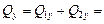
 .
. = 40∙(–1,39) = –55,6 Н.
= 40∙(–1,39) = –55,6 Н. Н= – 55,6 Н+ 2950 Н= 2894,4 Н.
Н= – 55,6 Н+ 2950 Н= 2894,4 Н.


