Однородные.
Линейные однородные ДУ 2-го порядка с постоянными коэффициентами имеют вид:
где р 1 и р 2 — действительные числа. Согласно теореме о структуре общего решения линейного однородного ДУ достаточно найти два линейно независимых частных решения
Где y00 – общее решение однородного уравнения. Будем искать решение уравнения (8) в виде Так как
Квадратное уравнение (9) называют характеристическим уравнением для ДУ (8), а его корни а) Корни
б) Корни
в) Корни
Пример 13. Найти общие решения линейных однородных ДУ 2-го порядка с постоянными коэффициентами: а) в) Решение. а)
Решим его, используя формулу корней квадратного уравнения:
Получим корни:
Поскольку
б) Характеристическое уравнение:
его корни найдем по формуле корней квадратного уравнения:
Поскольку
в) Характеристическое уравнение:
его корни найдем по формуле корней квадратного уравнения:
Получим комплексно сопряженные корни Решение запишем в виде (12):
г) Характеристическое уравнение:
Решим его:
|

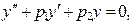 (8)
(8) и
и  уравнения (12), чтобы записать общее решение:
уравнения (12), чтобы записать общее решение: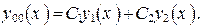
 где
где 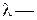 некоторая постоянная. Чтобы определить
некоторая постоянная. Чтобы определить  подставим
подставим 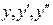 в уравнение (8).
в уравнение (8). 
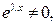 то
то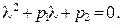 (9)
(9) и
и  характеристическими числами. При решении характеристического уравнения (9) могут возникнуть три случая:
характеристическими числами. При решении характеристического уравнения (9) могут возникнуть три случая: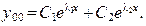 (10)
(10)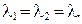 Общее решение уравнения (8) будет иметь вид:
Общее решение уравнения (8) будет иметь вид: (11)
(11) Тогда общее решение уравнения (8) примет вид:
Тогда общее решение уравнения (8) примет вид: (12)
(12) б)
б) 
 г)
г) 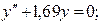
 Составим характеристическое уравнение:
Составим характеристическое уравнение:


 и
и  то общее решение запишем в виде (10):
то общее решение запишем в виде (10):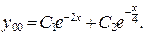

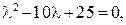

 то общее решение запишем в виде (11):
то общее решение запишем в виде (11):


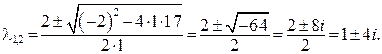
 где а =1, b =4.
где а =1, b =4.



 — комплексно сопряженные корни вида
— комплексно сопряженные корни вида 




