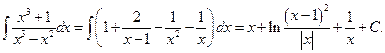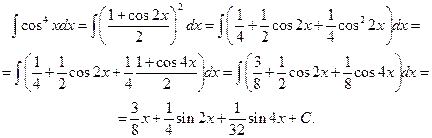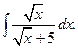Задача №6. (Комбинаторный метод вычисления вероятностей в классической схеме).
Варианты 1, 2 В магазин поступило n телевизоров. Из них k имеют скрытые дефекты. Покупателю для выбора наудачу предложено l телевизоров. Какова вероятность того, что все предложенные покупателю изделия не содержат дефектов? 1. n=30, k=3, l=2. 2. n=20, k=2, l=3. Варианты 3,4 Из партии, содержащей n изделий, среди которых k бракованных, наудачу извлекают m изделий для контроля. Найти вероятности следующих событий: А={в полученной выборке ровно l бракованных изделий}, B={в полученной выборке нет бракованных изделий}. 3. n=10, k=3, l=1, m=4. 4. n=12, k=3, l=2, m=5 Варианты 5,6 Имеются два ящика с деталями. В первом n деталей, из них m годных. Во втором ящике N изделий, из них M годных. Сборщик наудачу выбрал по одной детали из каждого ящика. Найти вероятность того, что обе выбранные детали годные. Какова вероятность того, что обе выбранные детали бракованные? 5. n=12, m=8, N=8, M=7. 6. n=14, m=10, N=6, M=4. Варианты 7,8 Группа, состоящая из 8 человек, занимает места с одной стороны прямоугольного стола. Найти вероятность того, что два определенных лица окажутся рядом, если: 7. число мест равно 8. 8. число мест равно 12. Варианты 9,10 Из урны, содержащей m+n шаров, из которых m белых и n черных, на удачу отбирают k шаров и откладывают в сторону. Найти вероятности следующих событий: A={все отложенные шары белые}, B={среди отложенных шаров ровно l белых}. 9. m=10, n=6, k=5, l=3. 10. m=8, n=12, k=6, l=4.
ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ КОНТРОЛЬНОЙ РАБОТЫ
Пример 1. Даны матрицы а) матрицу
Решение. а). Раскроем скобки, получим
Применяя правило умножения матрицы на матрицу, имеем
Следовательно,
б). Обратную матрицу
Обратная матрица определяется формулой:
Вычислим определитель матрицы, проверим, что матрица невырожденная, следовательно, имеет обратную матрицу. Определитель найдем, раскрывая по элементам первой строки:
Находим алгебраические дополнения элементов исходной матрицы
Итак, присоединенная матрица имеет вид:
Таким образом, обратная матрица равна
Проверим, что обратная матрица найдена правильно, должно выполняться условие
Пример 2. На плоскости даны вершины треугольника а). Канонические уравнения сторон б). Уравнение высоты, опущенной из вершины B; в). Внутренний угол г). Уравнение медианы, проведенной из вершины B; д). Расстояние от точки В до стороны
Решение. а). Уравнения сторон найдем, используя уравнение прямой, проходящей через две заданные точки:
б). Угловой коэффициент высоты
в). Для нахождения внутреннего угла
Получаем, г). Чтобы составить уравнение медианы, найдем координаты точки
д). Расстояние от вершины
точка, от которой определяется расстояние. Общее уравнение стороны Строим треугольник в координатных осях:
Пример 3. Найти производную а) г) Решение. а)
Используя определение производной, получаем
б) Применяя правила дифференцирования, получим
в) Применим формулу дифференцирования сложной функции:
г) Если в уравнение, задающее неявную функцию, подставить решение
Получили уравнение относительно неизвестной
д) Производную функции, заданной параметрически, определим по формуле
Получаем:
В задаче 4 требуется вычислить неопределенные интегралы. При этом интеграл в задании 4 а) вычисляется методом подведения выражений под знак дифференциала. Интеграл задания 4 б) относится к интегралам «группы четырех». Для приведения таких интегралов к табличным необходимо выделять в знаменателе подынтегральных дробей полные квадраты и применить далее соответствующую подстановку. Можно, также, сразу выполнить замену переменной интегрирования по такому правилу: новая переменная интегрирования равна старой переменной интегрировании плюс половина коэффициента при первой степени старой переменной интегрирования в приведенном квадратном трехчлене. Для решения примера 4 в) надо применить формулу интегрирования по частям:
В задании 4 г) требуется проинтегрировать дробно-рациональную функцию. Если дробь под интегралом неправильная, надо выделить сначала целую часть. Это можно сделать, например, с помощью приема деление многочлена на многочлен «уголком». Затем правильную дробь следует представить суммой простых дробей в соответствии с корнями знаменателя. Неизвестные вначале коэффициенты простых дробей определяются методом неопределенных коэффициентов. Интеграл 4д) содержит тригонометрические функции и решается соответствующей подстановкой. Замену переменной интегрирования необходимо выполнить и для решения последнего примера этой группы заданий. Подстановка должна быть такой, чтобы избавиться от иррациональностей. Приведем образцы решений примеров задачи 4, где более детально разъясняются вышеуказанные рекомендации. Пример 4. Вычислить неопределенный интеграл Решение.
Пример 5. Вычислить неопределенный интеграл Решение.
Пример 6. Вычислить неопределенный интеграл Решение.
Пример 7.
Вычислить неопределенный интеграл Решение. Выделяем сначала целую часть подынтегральной дроби:
Знаменатель правильной дроби имеет один простой корень Поэтому дробь заменим суммой простых дробей вида:
Неизвестные вначале коэффициенты находим следующим образом (метод неопределенных коэффициентов). Просуммируем дроби в правой части, приводя их к общему знаменателю. Сравнивая числители дробей, справа и слева, имеем тождество
Поочередно задавая удобные значения
Пример 8. Вычислить неопределенный интеграл Решение.
Пример 9. Вычислить неопределенный интеграл Решение.
|

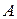 и
и  .
. 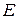 - единичная матрица. Найти:
- единичная матрица. Найти: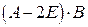 ; б) обратную матрицу
; б) обратную матрицу  и проверить, что
и проверить, что  :
: .
. .
. .
. .
. найдем, используя присоединенную матрицу
найдем, используя присоединенную матрицу  . Элементы присоединенной матрицы - это алгебраические дополнения соответствующих элементов матрицы
. Элементы присоединенной матрицы - это алгебраические дополнения соответствующих элементов матрицы 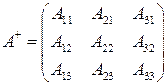 .
. .
. .
.
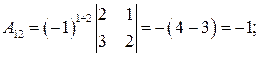
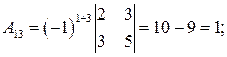

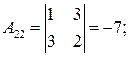

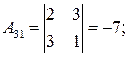
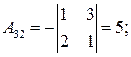
 .
. .
. .
.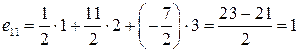 - верно,
- верно, - верно,
- верно, - верно.
- верно. . Найти:
. Найти: и
и 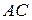 ;
;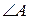 ;
; .
. .
.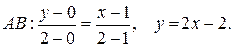
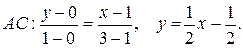 Угловой коэффициент прямой
Угловой коэффициент прямой 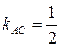 .
. связан с угловым коэффициентом стороны
связан с угловым коэффициентом стороны  . Отсюда находим,
. Отсюда находим, 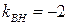 . Уравнение высоты составим, используя уравнение прямой, имеющей заданный наклон и проходящей через заданную точку:
. Уравнение высоты составим, используя уравнение прямой, имеющей заданный наклон и проходящей через заданную точку:  .
. .
. используем формулу
используем формулу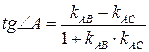 .
.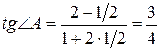 .
.  .
.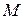 - середины стороны
- середины стороны  .
. (каноническое уравнение вертикальной прямой).
(каноническое уравнение вертикальной прямой).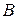 до стороны
до стороны 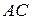 найдем по формуле:
найдем по формуле: , где
, где  - общее уравнение прямой,
- общее уравнение прямой, 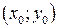 -
- . Поэтому
. Поэтому  .
.
 : а) исходя из определения производной функции
: а) исходя из определения производной функции  ; б) используя правила дифференцирования и формулы таблицы производных основных элементарных функций; в) сложной функции
; б) используя правила дифференцирования и формулы таблицы производных основных элементарных функций; в) сложной функции  ; г) функции, заданной в неявном виде; д) функции, заданной параметрически:
; г) функции, заданной в неявном виде; д) функции, заданной параметрически: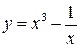 ; б)
; б) 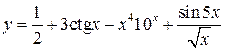 ; в)
; в) 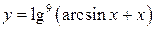 ;
; ; д)
; д)  .
.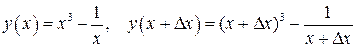 . Отсюда следует
. Отсюда следует
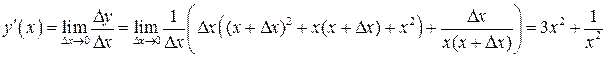 .
. .
. .
. .
. , то уравнение превращается в тождество. Тождество можно дифференцировать – равенство не нарушится. Дифференцируем обе части соотношения
, то уравнение превращается в тождество. Тождество можно дифференцировать – равенство не нарушится. Дифференцируем обе части соотношения 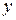 - функция
- функция 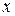 :
: ,
,  ,
,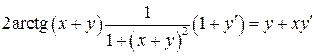 ,
,  ,
,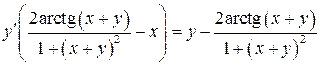 ,
, . Решая его, находим
. Решая его, находим .
.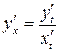 .
. .
. .
.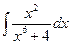 .
. .
.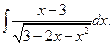
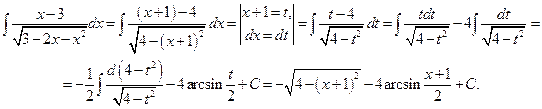
 .
.
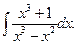
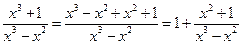 .
. и один кратный корень
и один кратный корень  .
. .
. .
. , составим уравнения для нахождения неизвестных коэффициентов. Пусть
, составим уравнения для нахождения неизвестных коэффициентов. Пусть  . Пусть
. Пусть  . Пусть
. Пусть 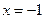 , тогда
, тогда  . Таким образом,
. Таким образом,  . Следовательно,
. Следовательно,