Теория вероятностей. 1. Элементы комбинаторики Размещениями m из n элементов называются m - элементные подмножества множества Е={a1,a2, ,an}
1. Элементы комбинаторики Размещениями m из n элементов называются m - элементные подмножества множества Е={ a1,a2,…,an }, различающиеся либо набором элементов, либо порядком их следования. Общее число таких различных комбинаций обозначается символом Перестановками называются размещения из n по n элементов. Общее число перестановок обозначают символом Сочетаниями из n по m элементов называются m- элементные подмножества множества Е={ a1,a2,…,an }, имеющие различный состав элементов. Два сочетания считаются различными, если хотя бы один элемент входит в одну комбинацию, но не входит в другую. Общее число различных сочетаний обозначают символом Число размещений, перестановок и сочетаний определяются формулами:
2. Классическое определение вероятности
3. Геометрическое определение вероятности
4. Основные свойства вероятности Вероятность любого события А - число, заключенное между 0 и 1. Вероятность невозможного события равна 0. Вероятность достоверного события равна 1. Сумма вероятностей противоположных событий равна 1:
Вероятность появления одного из двух несовместных событий равна сумме вероятностей этих событий:
Для любых двух событий A и B имеет место формула (теорема сложения для произвольных событий):
Для полной группы несовместных событий
Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
Если события А и В – независимые, то
5. Формула полной вероятности. Формулы Байеса Если известно, что событие А может произойти с одним из событий
Вероятности гипотез после того как имело место событие А переоценивают по формулам Байеса:
6. Если производится n независимых испытаний, в каждом из которых вероятность появления события А одна и та же и равна p (вероятность «успеха»), то вероятность того, что в этих n испытаниях событие А наступит ровно k раз, выражается формулой Бернулли:
Число k0 называется наивероятнейшим числом наступления события А в n испытаниях по схеме Бернулли, если значение не меньше остальных значений. Число
Пример 15. В ящике находится 10 деталей. Из них 3 дефектные. Наудачу отобраны 3 детали. Какова вероятность того, что: а) все детали дефектные (событие А); б) только одна деталь дефектная (событие В); в) все три детали годные (событие С); г) хотя бы одна деталь дефектная (событие D). Решение. Используем классическое определение вероятности. а) Событие А = {выбранные три детали дефектные};
Элементарное событие в данной задаче - комбинация (сочетание) из трех деталей.
б) Событие В = {из трех выбранных деталей 1 деталь дефектная, две детали без дефекта};
где Следовательно, в) Событие С = {выбранные три детали бездефектные}
г) Событие D = {хотя бы одна из трех выбранных деталей бездефектная}. Рассмотрим противоположное событие
|

 .
. .
. .
.
 , где n – общее число элементарных событий (исходов, которые в данном опыте образуют конечную полную группу равновозможных попарно несовместных событий), m – число элементарных событий, благоприятствующих наступлению события А.
, где n – общее число элементарных событий (исходов, которые в данном опыте образуют конечную полную группу равновозможных попарно несовместных событий), m – число элементарных событий, благоприятствующих наступлению события А. . Вероятность попадания точки в какую либо часть А области Ω; пропорциональна мере (длине, площади, объему и т.д.) этой части и не зависит от ее расположения и формы.
. Вероятность попадания точки в какую либо часть А области Ω; пропорциональна мере (длине, площади, объему и т.д.) этой части и не зависит от ее расположения и формы.

 .
.

 - теорема умножения.
- теорема умножения. - теорема умножения.
- теорема умножения. (гипотез), образующих полную группу попарно несовместных событий, то вероятность события А определяется по формуле полной вероятности:
(гипотез), образующих полную группу попарно несовместных событий, то вероятность события А определяется по формуле полной вероятности:


 при
при 
 можно найти из двойного неравенства:
можно найти из двойного неравенства: .
.
 - общее число способов выбрать 3
- общее число способов выбрать 3  детали из имеющихся 10 деталей.
детали из имеющихся 10 деталей.  (имеется всего один вариант выбора 3 дефектных деталей)
(имеется всего один вариант выбора 3 дефектных деталей) .
.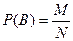 ,
, - количество вариантов, благоприятствующих появлению события В, при которых 1 дефектная деталь выбирается из группы 3 дефектных и 2 бездефектные детали выбираются из группы 7 бездефектных деталей
- количество вариантов, благоприятствующих появлению события В, при которых 1 дефектная деталь выбирается из группы 3 дефектных и 2 бездефектные детали выбираются из группы 7 бездефектных деталей  .
. .
. .
. = { среди трех выбранных деталей нет дефектных}. Так как
= { среди трех выбранных деталей нет дефектных}. Так как  , то
, то  .
.


