Теория вероятностей и математическая статистика.
Понятие случайного события, алгебра событий. Классическое, геометрическое, статистическое и абстрактное определения вероятности. Некоторые понятия комбинаторики: размещения, перестановки и сочетания. Свойства вероятности. Теорема сложения. Условная вероятность, теорема умножения. Независимость событий. Формула полной вероятности и формулы Байеса. Схема независимых испытаний Бернулли, формула Бернулли. Предельные теоремы в схеме Бернулли. Понятие случайной величины, дискретные и непрерывные случайные величины. Способы их задания. Числовые характеристики случайных величин – математические ожидание и дисперсия, их свойства и формулы вычисления. Нормальное распределение как важнейший пример непрерывных распределений, нормальная кривая. Понятие выборки. Выборочные характеристики – выборочное среднее, выборочная дисперсия, исправленная выборочная дисперсия. Точечные оценки. Интервальные оценки. Литература: 1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. -М.: Наука, 1984. 2. Волокитин Г.И., Ларченко В.В., Азаров Д.А., Редько Ю.С. Начала линейной алгебры. Учебное пособие. – Ростов-на-Дону: Издательский центр ДГТУ, 2012. 3. Я.С. Бугров, С.М. Никольский. Элементы линейной алгебры и аналитическая геометрия. Москва «Наука». Главная редакция физико-математической литературы, 1980. 4. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия. Издание четвертое, дополненное. Москва «Наука» Главная редакция физико-математической литературы, 1973. 5. А.Ф. Бермант, И.Г. Араманович. Краткий курс математического анализа для втузов. Москва: “Наука”. Главная редакция физико-математической литературы, 1973. 6. Г.М. Берман, Сборник задач по курсу математического анализа (для втузов). Москва: “Наука”. 1985. 7. П. Е. Данко, и др. Высшая математика в упражнениях и задачах: Учебное пособие для втузов. В 2-х ч. 1980 – ч.1, 1984 – ч.2. 8. Пискунов Н.С. Дифференциальное и интегральное исчисления. Т.1. – М.: Интеграл-Пресс, 2005. 9. Ворович Е.И., Глушкова В.Н., Тукодова О.М., Федосеев В.Б. Введение в математический анализ. Понятие производной. Учебное пособие. – Ростов н/Д. Издательский центр ДГТУ, 2012. 10. Мишняков Н.Т., Ароева Г.А., Коровина К.С. Приложение производной к исследованию функций. Учебное пособие. – Ростов н/Д. Издательский центр ДГТУ, 2012. 11. Гмурман В. Е. Теория вероятностей и математическая статистика. - М.: Высшая школа, 1998. 12. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике. – М: Высшая школа, 1999.
ВАРИАНТЫ ЗАДАНИЙ КОНТРОЛЬНОЙ РАБОТЫ Задача 1. Даны матрицы а) матрицу 1. 3. 5. 7. 9. 10. Задача 2. На плоскости даны вершины треугольника а). Канонические уравнения сторон б). Уравнение высоты, опущенной из вершины B; в). Внутренний угол г). Уравнение медианы, проведенной из вершины B; д). Расстояние от точки В до стороны 1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
Задача 3. Найти производную Вариант 1. а) г ) Вариант 2. а) г) Вариант 3. а) в) г) Вариант 4. а) в) г)
Вариант 5. а) г)
Вариант 6. а) г) Вариант 7. а) в) г) Вариант 8. а) в) г) Вариант 9. а) в) г)
Вариант 10.
а) г) Задача 4. Вычислить неопределенные интегралы:
Вариант 1. а) г)
Вариант 2. а) г)
Вариант 3. а) г)
Вариант 4. а) г)
Вариант 5. а) г)
Вариант 6. а) г)
Вариант 7. а) г)
Вариант 8. а) г)
Вариант 9. а) г)
Вариант 10. а) г)
|

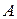 и
и  .
. 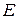 - единичная матрица. Найти:
- единичная матрица. Найти: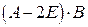 ; б) обратную матрицу
; б) обратную матрицу  и проверить, что
и проверить, что  :
: ; 2.
; 2.  ;
;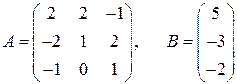 ; 4.
; 4.  ;
; ; 6.
; 6.  ;
; ; 8.
; 8.  ;
; ;
; .
. . Найти:
. Найти: и
и 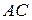 ;
;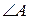 ;
; ;
;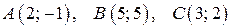 ;
; ;
;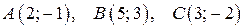 ;
; ;
; ;
; ;
; ;
; ;
; .
. : а) исходя из определения производной функции
: а) исходя из определения производной функции  ; б) используя правила дифференцирования и формулы таблицы производных основных элементарных функций; в) сложной функции
; б) используя правила дифференцирования и формулы таблицы производных основных элементарных функций; в) сложной функции  ; г) функции, заданной в неявном виде; д) функции, заданной параметрически:
; г) функции, заданной в неявном виде; д) функции, заданной параметрически: ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  .
. ; б)
; б) 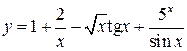 ; в)
; в) 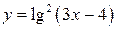 ;
; ; д)
; д)  .
.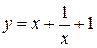 ; б)
; б)  ;
; ;
; ; д)
; д)  .
. ; б)
; б)  ;
;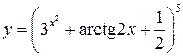 ;
; ; д)
; д)  .
. ; б)
; б)  ; в)
; в) 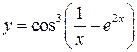 ;
; ; д)
; д)  .
. ; б)
; б) 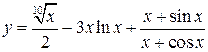 ; в)
; в) 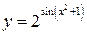 ;
; ; д)
; д)  .
.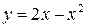 ; б)
; б)  ;
; ;
; ; д)
; д)  .
. ; б)
; б) 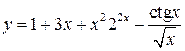 ;
;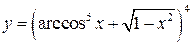 ;
; ; д)
; д)  .
. ; б)
; б)  ;
; ;
;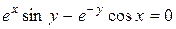 ;д )
;д )  .
. ; б)
; б)  ; в)
; в)  ;
;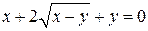 ; д)
; д)  .
. ; б)
; б)  ; в)
; в)  ;
;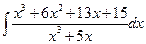 ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  ; в)
; в) 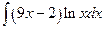 ;
; ; д)
; д)  ; е)
; е) 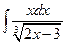 .
. ; б)
; б)  ; в)
; в) 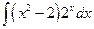 ;
; ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 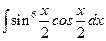 ; е)
; е)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 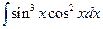 ; е)
; е) 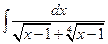 .
. ; б)
; б)  ; в)
; в)  ;
; ; д)
; д) 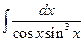 ; е)
; е)  .
.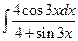 ; б)
; б)  ; в)
; в)  ;
; ; д)
; д)  ; е)
; е)  .
.


