ИНТЕРФЕРЕНЦИЯ И ДИФРАКЦИЯ СВЕТА. ПРИНЦИП РЕНТГЕНОСТРУКТУРНОГО АНАЛИЗА.
1. Интерференция световых волн. Когерентность. Наложение двух или нескольких волн, приводящее к устойчивому во времени усилению колебаний в одних точках пространства и ослаблению в других, называется интерференцией. В обычных условиях довольно часто встречается наложение световых волн от различных источников, но интерференции света не наблюдается. Каждый такой источник (лампа, пламя, Солнце и др.) представляет собой совокупность огромного количества излучаемых атомов. Разность фаз колебаний, излучаемых такими источниками, не будет постоянной, а быстро и беспорядочно меняется во времени. Интерференция света может возникать только от согласованных когерентных источников, которые обеспечивают постоянную во времени разность фаз Dj слагаемых волн в различных точках. Волны, отвечающие этому условию, называются когерентными, т.е. при одинаковой частоте (длине волны) имеют постоянную разность фаз. Интерференция могла быть осуществлена от двух синусоидальных волн одинаковой частоты. Можно получить когерентные волны, разделив волну от одного источника на две части (путем отражения или преломления) и затем свести эти две волны вместе.
Второй способ получения когерентных источников основан на отражении света от двух плоских зеркал, установленных под углом a, близким к 1800. Эта оптическая система называется зеркалами Френеля. Когерентными источниками служат мнимые изображения S1 и S2
возникает в точке P. Еще один способ заключается в получении мнимого изображения S¢ источника S c помощью специального однослойного зеркала (зеркало Ллойда). Источники S и S¢ (рис.3) можно рассматривать как когерентные. Они создают интерференционную картину в точке A экрана Э. Для монохроматического света интерференционная картина представляет ряд чередующихся темных и светлых полос (максимумы и минимумы). В случае белого (немонохроматического) света максимумы для разных l располагаются в разных местах, из-за чего интерференционные полосы расширяются и приобретают радужную окраску. Образование когерентных волн и их интерференция происходит также при попадании света на тонкую прозрачную пластинку или пленку. За счет отражения света от обеих поверхностей пленки происходит расщепление падающего светового луча и создаются условия для интерференции. Этим объясняется, в частности, появление радужной окраски мыльных пузырей, пленки маслянистых веществ на поверхности воды, крыльев бабочек и других насекомых, внутренней поверхности раковин, перьев некоторых птиц (колибри, павлины).
Сложение гармонических колебаний одного направления и одинаковой частоты с разностью фаз
а для рассматриваемого нами случая:
Из формулы Определим: Если свет распространяется в среде с показателем преломления n, то:
Подставляя в формулу (2) значения Dj, получим:
т.е. Е зависит от значения D. В точках, где D равна нечётному числу длин полуволн, т.е.:
2. Дифракция света. Дифракция света на щели в параллельных лучах. При распространении волн в среде, содержащей неоднородности, наблюдается явление, называемое дифракцией. Сущность его состоит в том, что волна, встречая на своем пути препятствие, огибает его, изменяя направление своего распространения. Возможность наблюдения дифракции зависит от соотношения длины волны света и размеров препятствия. Явление дифракции проявляется сильнее, если размеры препятствия (щели) сравнимы с длиной волны l. Явление дифракции света в природных условиях почти не наблюдается. Это связано с тем, что размеры большей части окружающих нас тел несоизмеримы с длиной волны света. Вследствие дифракции теневое изображение объекта перестает быть подобным самому предмету.
Если между экраном Э и источником монохроматического света S поместить другой непрозрачный экран A с малым отверстием d, то граница геометрической тени не будет резкой. Это особенно заметно, когда размер d отверстия очень мал по сравнению с расстоянием L от экрана до отверстия (d<<L). Тогда пятно на экране будет представлено в виде системы чередующихся светлых и тёмных колец, постепенно переходящих друг в друга, захватывающих область геометрической тени, а также выходящих за её пределы. Это говорит о непрямолинейном распространении света от источника S, о загибании световых волн у краёв отверстия в экране A. При использовании белого света дифракционная картина приобретает радужную окраску. Дифракцией света объясняется появление радужных колец вокруг источника света, когда воздух насыщен туманом или пылью, окраска жемчуга (дифракция белого света на содержащихся в нём инородных мельчайших вкраплениях).
В зависимости от разности хода лучей на экране A в точках c; d и т.д. возникнут интерференционные максимумы и минимумы, т.е. кольцеобразная дифракционная картина. Для того чтобы определить результат дифракции в некоторой точке пространства, следует рассчитать, согласно принципу Гюйгенса-Френеля, интерференцию вторичных волн, попавших в эту точку от волновой поверхности. Для волновой поверхности произвольной формы такой расчёт достаточно сложен. Но в отдельных случаях (сферическая или плоская волновая поверхность, симметричное расположение точки относительно волновой поверхности S1, и непрозрачной преграды A) вычисления сравнительно просты. Волновую поверхность при этом разбивают на отдельные участки – зоны Френеля, расположенные определённым образом, что упрощает математический расчёт.
На рис.7 показан случай, когда m=2, что соответствует в точке M дифракционному минимуму. Таким образом, на экране Э получится система светлых (максимумов) и тёмных (минимумов) полос, симметрично расположенных влево и вправо от центральной (φ=0) наиболее яркой полосы. Интенсивность J остальных максимумов убывает по мере удаления от центрального максимума (см. рис.7). Если щель освещается белым светом, то на экране Э образуется система цветных полос, лишь центральный максимум будет сохранять цвет падающего света, так как при φ=0 усиливаются все длины волн света.
3. Дифракционная решётка. Дифракционный спектр.
Рассмотрим лучи, падающие на левые края щелей (N=3). Благодаря дифракции свет от щелей будет распространяться во всевозможных направлениях. Разность хода лучей от крайних точек двух соседних щелей и дифрагирующих под углом φ будет определяться: Максимумы будут располагаться симметрично относительно центрального (k=0; φ=0). Выражение
Таким образом, дифракционная решётка разлагает сложный свет в спектр и поэтому с успехом применяется в спектральных приборах, например, дифракционном спектроскопе – приборе, служащим для измерения длины световых волн, т.е. для проведения спектрального анализа.
4. Дифракция электромагнитных волн на пространственных структурах. Основы рентгеноструктурного анализа.
Дифракция волн может происходить на мелких неоднородностях и частицах. Наиболее простым является случай, когда неоднородности образуют периодическую структуру. Дифракционные решётки могут служить примером периодической структуры. Естественной 3-х мерной структурой являются кристаллы, в которых рассеивающими центрами служат узлы (атомы, ионы) кристаллической решётки. В кристалле можно выделить направления, вдоль которых дафрагированные волны усиливают друг друга. Пучок монохроматического излучения, пройдя сквозь такую структуру, образует на экране плоскостную двухмерную дифракционную картину – систему светлых пятен (максимумов), расположенных в определённом порядке. По расположению этих максимумов, их относительной интенсивности, длине волны можно на основе соответствующих расчётов определить пространственную 3-х мерную структуру объекта, обусловившего дифракцию. В качестве таких объектов могут быть крупные молекулы, в том числе и биомакромолекулы. Однако чёткую дифракционную картину можно получить только в том случае, если период структуры d будет несколько больше длины волны λ (d>λ). Это ограничение не позволяет осуществить дифракцию света на кристаллах, так как период кристаллической решётки (расстояние между плоскостями кристалла) в тысячи раз (~10-10 м) меньше длины световой волны. Однако для рентгеновских лучей условие d>λ выполняется. В 1912 году М.ЛАУЭ, пропустив узкий пучок рентгеновских лучей, выделенный свинцовыми диафрагмами, через монокристалл (кристалл играет роль пространственной решётки), получил на фотопластинке дифракционную картину (лауэграмма) в виде тёмных пятен (дифракционные максимумы). Порядок расположения частиц в решётке кристалла определяет порядок и симметрию в расположении дифракционных максимумов.
где k= ±1; ±2; ±3;… - порядок максимумов. Это формула Вульфа-Брэгга. При падении монохроматического рентгеновского излучения на кристалл под различными углами максимум будет иметь место для углов, отвечающих формуле Вульфа-Брэгга. Угол θ измеряется на фотографии дифракционной картины (по положению дифракционных максимумов). Рентгеноструктурный анализ – это метод, который по дифракционной картине, полученной на неизвестной кристаллической структуре при помощи рентгеновских лучей известной длины, позволяет найти расположение частиц, составляющих эту структуру (определить d). Он имеет большое практическое значение для биологии, поскольку является наиболее эффективным методом определения пространственной структуры кристаллических соединений. Для монокристалла обычно используется метод “вращения кристалла” (рис.12). При повороте кристалла разные системы плоскостей попадают под падающий пучок рентгеновских лучей в положение, при котором удов
ЛЕКЦИЯ №21
|

 Излучаемые одной системой атомов, полученные таким способом две волны будут когерентны и при наложении могут интерферировать. На практике разделение одной световой волны на две можно осуществить посредством непрозрачного экрана с двумя небольшими отверстиями. В соответствии с принципом Гюйгенса-Френеля источник S (рис.1) создает в отверстиях экрана источники вторичных волн S1 и S2. Очевидно, что всякое изменение фазы волн, излучаемых источником S, сопровождается точно такими же изменениями фаз волн, излучаемых вторичными источниками S1 и S2, т.е. у волн этих источников разность фаз все время остается неизменной, и источники являются когерентными.
Излучаемые одной системой атомов, полученные таким способом две волны будут когерентны и при наложении могут интерферировать. На практике разделение одной световой волны на две можно осуществить посредством непрозрачного экрана с двумя небольшими отверстиями. В соответствии с принципом Гюйгенса-Френеля источник S (рис.1) создает в отверстиях экрана источники вторичных волн S1 и S2. Очевидно, что всякое изменение фазы волн, излучаемых источником S, сопровождается точно такими же изменениями фаз волн, излучаемых вторичными источниками S1 и S2, т.е. у волн этих источников разность фаз все время остается неизменной, и источники являются когерентными.

 Выполним расчет интерференционной картины, когда две когерентные волны от источников S1 и S2 проходят разные пути r1 и r2 и интерферируют в точке М (рис.4), т.е. между ними возникает разность хода D=r2 – r1 (геометрическая разность хода). Если волны распространяются в среде с показателем преломления n, то говорят об оптической разности хода d=nD. Колебания векторов электрической напряженности E в точке М, удаленной от источников на расстояния r1 и r2 соответственно от каждого источника, происходит по гармоническому закону (амплитуды обоих колебаний примем одинаковыми и обозначим через Em). Тогда
Выполним расчет интерференционной картины, когда две когерентные волны от источников S1 и S2 проходят разные пути r1 и r2 и интерферируют в точке М (рис.4), т.е. между ними возникает разность хода D=r2 – r1 (геометрическая разность хода). Если волны распространяются в среде с показателем преломления n, то говорят об оптической разности хода d=nD. Колебания векторов электрической напряженности E в точке М, удаленной от источников на расстояния r1 и r2 соответственно от каждого источника, происходит по гармоническому закону (амплитуды обоих колебаний примем одинаковыми и обозначим через Em). Тогда 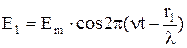 ,
,  .
. , как было показано ранее, дает результирующие колебания той же частоты. Амплитуда результирующего колебания светового вектора выражается в виде:
, как было показано ранее, дает результирующие колебания той же частоты. Амплитуда результирующего колебания светового вектора выражается в виде: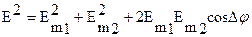 , (1)
, (1) . (2)
. (2)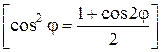 следует, что
следует, что  .
. .
.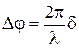 .
. ,
,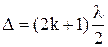 , k=0,1,2,3,…, значение
, k=0,1,2,3,…, значение  и амплитуда результирующего колебания равна нулю. В этих точках образуются интерференционные минимумы. Если разность хода равна четному числу длин полуволн (или целому числу длин волн)
и амплитуда результирующего колебания равна нулю. В этих точках образуются интерференционные минимумы. Если разность хода равна четному числу длин полуволн (или целому числу длин волн)  , то
, то  , а Е=2Еm (интерференционный максимум).
, а Е=2Еm (интерференционный максимум). В опыте дифракцию можно наблюдать при образовании тени от препятствия в виде тонкой проволочки или волоска, а также при прохождении света через отверстие весьма малого размера (доли с миллиметра) (рис.5).
В опыте дифракцию можно наблюдать при образовании тени от препятствия в виде тонкой проволочки или волоска, а также при прохождении света через отверстие весьма малого размера (доли с миллиметра) (рис.5). Дифракция определяется волновыми свойствами света, и объяснить это явление можно с помощью принципа Гюйгенса-Френеля, согласно которому точки среды, которых достиг фронт волны, являются источниками элементарных вторичных волн, которые когерентны. Пусть свет от источника S падает на экран A через круглое отверстие “ab” в экране B (рис.6). Каждая точка участка “ab” фронта световой волны S1, является вторичным источником света. Вторичные источники когерентны, поэтому исходящие от них лучи (волны) 1,2; 3,4; и т.д. будут интерферировать между собой.
Дифракция определяется волновыми свойствами света, и объяснить это явление можно с помощью принципа Гюйгенса-Френеля, согласно которому точки среды, которых достиг фронт волны, являются источниками элементарных вторичных волн, которые когерентны. Пусть свет от источника S падает на экран A через круглое отверстие “ab” в экране B (рис.6). Каждая точка участка “ab” фронта световой волны S1, является вторичным источником света. Вторичные источники когерентны, поэтому исходящие от них лучи (волны) 1,2; 3,4; и т.д. будут интерферировать между собой. Рассмотрим результат дифракции плоской монохроматической волны на щели, вырезанной в непрозрачной преграде (рис.7) и имеющей постоянную ширину BC=a. Волна падает нормально щели в виде плоскопараллельного пучка света. Все точки волновой поверхности, открытые щелью, являются центром вторичных волн, распространяющихся за щелью по всем направлениям. Изобразить все эти вторичные волны невозможно, поэтому на рис.7 показаны только вторичные волны, распространяющиеся под углом φ. Лучи, дифрагирующие под углом φ, будут собраны в точке M экрана и интерферируют. При φ=0 все волны придут в точку M0 в одинаковой фазе и усилят друг друга, на экране появится наиболее светлая полоса – центральный максимум. Чтобы определить результат интерференции при φ≠0, из точки B проведём перпендикуляр BD к направлению пучка вторичных волн. Оптические пути лучей от BD до точки M экрана одинаковы (линза L дополнительной разности хода не вносит), поэтому разность хода DC крайних лучей равна:
Рассмотрим результат дифракции плоской монохроматической волны на щели, вырезанной в непрозрачной преграде (рис.7) и имеющей постоянную ширину BC=a. Волна падает нормально щели в виде плоскопараллельного пучка света. Все точки волновой поверхности, открытые щелью, являются центром вторичных волн, распространяющихся за щелью по всем направлениям. Изобразить все эти вторичные волны невозможно, поэтому на рис.7 показаны только вторичные волны, распространяющиеся под углом φ. Лучи, дифрагирующие под углом φ, будут собраны в точке M экрана и интерферируют. При φ=0 все волны придут в точку M0 в одинаковой фазе и усилят друг друга, на экране появится наиболее светлая полоса – центральный максимум. Чтобы определить результат интерференции при φ≠0, из точки B проведём перпендикуляр BD к направлению пучка вторичных волн. Оптические пути лучей от BD до точки M экрана одинаковы (линза L дополнительной разности хода не вносит), поэтому разность хода DC крайних лучей равна: 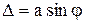 . Разбиваем DC на отрезки, равные λ/2 (на рисунке показано 2 отрезка). В общем случае эта разность хода содержит m полуволн:
. Разбиваем DC на отрезки, равные λ/2 (на рисунке показано 2 отрезка). В общем случае эта разность хода содержит m полуволн:  . Проведём из точки
. Проведём из точки  прямую
прямую 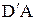 , параллельную BD и разделим BC на две равные зоны Френеля BA=AC. Любой вторичной волне, идущей от какой-либо точки одной зоны Френеля, можно найти в соседних зонах такие вторичные волны, что разность хода между ними будет λ/2. Например, вторичная волна, идущая от точки C в выбранном направлении проходит до точки M расстояние на λ/2 больше, чем волна, идущая из точки A и т.д. Следовательно, вторичные волны, идущие от двух соседних зон, погасят друг друга, т.к. различаются по фазе на π. Число зон, укладывающихся в щели, зависит от длины волны λ и угла φ. Если щель BC разбита при построении на нечётное число зон Френеля m=(2k+1), а DC на нечётное число отрезков, равных λ/2, то в точке M наблюдается дифракционный максимум, т.е.:
, параллельную BD и разделим BC на две равные зоны Френеля BA=AC. Любой вторичной волне, идущей от какой-либо точки одной зоны Френеля, можно найти в соседних зонах такие вторичные волны, что разность хода между ними будет λ/2. Например, вторичная волна, идущая от точки C в выбранном направлении проходит до точки M расстояние на λ/2 больше, чем волна, идущая из точки A и т.д. Следовательно, вторичные волны, идущие от двух соседних зон, погасят друг друга, т.к. различаются по фазе на π. Число зон, укладывающихся в щели, зависит от длины волны λ и угла φ. Если щель BC разбита при построении на нечётное число зон Френеля m=(2k+1), а DC на нечётное число отрезков, равных λ/2, то в точке M наблюдается дифракционный максимум, т.е.:  , где k=0,±1, ±2,… - порядок максимума. Условие же дифракционных минимумов:
, где k=0,±1, ±2,… - порядок максимума. Условие же дифракционных минимумов: (m=2k).
(m=2k). Дифракционная решётка – это оптическое устройство, представляющее собой стеклянную пластинку, на которой алмазным остриём наносится большое количество параллельных штрихов с промежутками между ними. Неповреждённое стекло между штрихами служит щелями решётки. Суммарную ширину щели “a” (рис.8) и промежутка “b” между щелями называют постоянной или периодом дифракционной решётки: d=a+b. Лучшие дифракционные решётки имеют до 1200-1500 штрихов на миллиметр (n), период дифракционной решётки
Дифракционная решётка – это оптическое устройство, представляющее собой стеклянную пластинку, на которой алмазным остриём наносится большое количество параллельных штрихов с промежутками между ними. Неповреждённое стекло между штрихами служит щелями решётки. Суммарную ширину щели “a” (рис.8) и промежутка “b” между щелями называют постоянной или периодом дифракционной решётки: d=a+b. Лучшие дифракционные решётки имеют до 1200-1500 штрихов на миллиметр (n), период дифракционной решётки  , общее число штрихов дифракционной решётки обозначают буквой N.
, общее число штрихов дифракционной решётки обозначают буквой N. Рассмотрим дифракцию (рис.9) плоской монохроматической волны, падающей нормально на дифракционную решётку. Если на решётку падает пучок монохроматических лучей, то вторичные волны, идущие от щелей по всем направлениям, являются когерентными и будут интерферировать, образуя дифракционную картину. Если между экраном и дифракционной решёткой поместить собирающую линзу L (экран расположен в фокальной плоскости линзы), то возникает дифракционная картина, являющаяся результатом двух процессов: дифракции света от каждой отдельной щели и интерференции света от щелей. Основные черты этого процесса определяются вторым явлением.
Рассмотрим дифракцию (рис.9) плоской монохроматической волны, падающей нормально на дифракционную решётку. Если на решётку падает пучок монохроматических лучей, то вторичные волны, идущие от щелей по всем направлениям, являются когерентными и будут интерферировать, образуя дифракционную картину. Если между экраном и дифракционной решёткой поместить собирающую линзу L (экран расположен в фокальной плоскости линзы), то возникает дифракционная картина, являющаяся результатом двух процессов: дифракции света от каждой отдельной щели и интерференции света от щелей. Основные черты этого процесса определяются вторым явлением.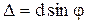 . Если эта разность хода будет равна нулю или целому числу длин волн, то при интерференции возникают главные максимумы, для которых выполняется условие:
. Если эта разность хода будет равна нулю или целому числу длин волн, то при интерференции возникают главные максимумы, для которых выполняется условие:  , где k – порядок главных максимумов (k=0; ±1; ±2; ±3;…). При выполнении условия
, где k – порядок главных максимумов (k=0; ±1; ±2; ±3;…). При выполнении условия  - будут возникать интерференционные минимумы.
- будут возникать интерференционные минимумы. ; J~N2.
; J~N2. Если на решётку падает белый свет, то для всех значений длин волн положение максимумов нулевого порядка совпадают (k=0; φ=0), положение же максимумов более высокого порядка будут различны (чем больше λ, тем больше φ) для данного значения k. Поэтому центральный максимум будет иметь вид узкой белой полоски (рис.10), а каждый из боковых максимумов представляет собой разноцветную полоску конечной ширины. Все спектры симметричны относительно нулевого максимума и обращены к нему коротковолновым Ф (фиолетовым) краем. Наиболее интенсивным является спектр 1-го порядка (k=1). Спектры боле высоких порядков менее интенсивны и, кроме того, могут накладываться друг на друга.
Если на решётку падает белый свет, то для всех значений длин волн положение максимумов нулевого порядка совпадают (k=0; φ=0), положение же максимумов более высокого порядка будут различны (чем больше λ, тем больше φ) для данного значения k. Поэтому центральный максимум будет иметь вид узкой белой полоски (рис.10), а каждый из боковых максимумов представляет собой разноцветную полоску конечной ширины. Все спектры симметричны относительно нулевого максимума и обращены к нему коротковолновым Ф (фиолетовым) краем. Наиболее интенсивным является спектр 1-го порядка (k=1). Спектры боле высоких порядков менее интенсивны и, кроме того, могут накладываться друг на друга. Дифракцию рентгеновских лучей можно наблюдать при отражении от кристалла (рис.11). Лучи 1 и 2 интерферируют, отразившись от двух соседних слоёв (d – расстояние между соседними атомными слоями). Разность хода Δ=DB+BC лучей будет равна
Дифракцию рентгеновских лучей можно наблюдать при отражении от кристалла (рис.11). Лучи 1 и 2 интерферируют, отразившись от двух соседних слоёв (d – расстояние между соседними атомными слоями). Разность хода Δ=DB+BC лучей будет равна 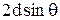 , где θ – угол скольжения. Эти волны усиливают друг друга, т.е. образуют максимумы в направлениях, для которых разность хода кратна λ. Поэтому можно записать:
, где θ – угол скольжения. Эти волны усиливают друг друга, т.е. образуют максимумы в направлениях, для которых разность хода кратна λ. Поэтому можно записать: , (3)
, (3) летворяется условие (3). Это значит, что при определённых углах θ на фотопластинке появятся дифракционные максимумы. Зная λ и определив из опыта θ и порядок спектра k, по формуле (3) рассчитывают расстояние d между соответствующими слоями структурных частиц.
летворяется условие (3). Это значит, что при определённых углах θ на фотопластинке появятся дифракционные максимумы. Зная λ и определив из опыта θ и порядок спектра k, по формуле (3) рассчитывают расстояние d между соответствующими слоями структурных частиц. Для веществ в мелкокристаллическом состоянии используют метод порошков (метод Дебая и Шерара) (рис.13), основанный на дифракции монохроматических рентгеновских лучей в поликристаллических телах (спрессованные порошки). Среди большого числа мелких кристаллов всегда найдутся такие, для которых выполняется условие (3). Так как условие (3) одинаково для многих кристаллов, по разному ориентированных, то дифрагированные лучи образуют в пространстве конус, вершина которого лежит в исследуемом объекте, а угол равен 4θ. Для другой совокупности d, k, θ, удовлетворяющей условию (3), будет соответствовать другой конус. На фотоплёнке рентгеновские лучи образуют рентгенограмму (дебаеграмму) в виде концентрических окружностей. Рентгенострукрурный анализ широко применяется при исследовании структуры биологических молекул (ДНК, белков). Описанным методом расшифрованы пространственные структуры гемоглобина, лизоцина, химотрипсина, рибонуклеазы. Основываясь на анализе рентгенограмм, Ф.Крик, Дж.Уотсон воспроизвели пространственную структуру ДНК и были удостоены Нобелевской премии. С помощью рентгеноструктурного анализа удалось понять, как функционируют молекулы ферментов, выяснить структурную основу многих наследственных заболеваний, структуру вирусов и т.д.
Для веществ в мелкокристаллическом состоянии используют метод порошков (метод Дебая и Шерара) (рис.13), основанный на дифракции монохроматических рентгеновских лучей в поликристаллических телах (спрессованные порошки). Среди большого числа мелких кристаллов всегда найдутся такие, для которых выполняется условие (3). Так как условие (3) одинаково для многих кристаллов, по разному ориентированных, то дифрагированные лучи образуют в пространстве конус, вершина которого лежит в исследуемом объекте, а угол равен 4θ. Для другой совокупности d, k, θ, удовлетворяющей условию (3), будет соответствовать другой конус. На фотоплёнке рентгеновские лучи образуют рентгенограмму (дебаеграмму) в виде концентрических окружностей. Рентгенострукрурный анализ широко применяется при исследовании структуры биологических молекул (ДНК, белков). Описанным методом расшифрованы пространственные структуры гемоглобина, лизоцина, химотрипсина, рибонуклеазы. Основываясь на анализе рентгенограмм, Ф.Крик, Дж.Уотсон воспроизвели пространственную структуру ДНК и были удостоены Нобелевской премии. С помощью рентгеноструктурного анализа удалось понять, как функционируют молекулы ферментов, выяснить структурную основу многих наследственных заболеваний, структуру вирусов и т.д.


