Прямой и плоскости общего положения
Решение частных случаев задачи на определение точки пересечения прямой с плоскостью основано на свойствах проекций геометрических образов частного положения. Задача 5.2. Построение точки пересечения прямой общего положения с проецирующей плоскостью (рис. 5.20).
1. Опустить перпендикуляр линии связи из точки М2 до пересечения с а1. Получим точку М1. 2. Показать видимость прямой а: полупрямая, находящаяся выше плоскости P (Р2), будет видимой на горизонтальной плоскости проекций до точки М пересечения с плоскостью. Задача 5.3. Построение точки пересечения проецирующей прямой с плоскостью общего положения(рис. 5.21). Алгоритм построения. 1. Через точку m1 провести фронталь f1 плоскости точки P(ΔABC), m1=E1, E1Р(ΔABC). Точка Е1 – горизонтальная проекция искомой точки пересечения прямой m с плоскостью P(ΔABC). 2. Построить f2, Е2Ì f2,f2∩m2=Е2. Точка Е2 – фронтальная проекция искомой точки пересечения прямой m с плоскостью P(ΔABC). 3. Показать видимость прямой m относительно точки Е по конкурирующим точкам.
Таким образом, признак перпендикулярности прямой и плоскости можно сформулировать так: прямая перпендикулярна плоскости, если ее горизонтальная проекция перпендикулярна к горизонтальной проекции горизонтали плоскости, а фронтальная проекция прямой перпендикулярна к фронтальной проекции фронтали плоскости.
1. Построить фронталь и горизонталь плоскости: h(h1; h2),f(f1; f2). 2. Из точки D1 провести перпендикуляр к горизонтальной проекции горизонтали, D1K1 h1. Из точки D2 провести перпендикуляр к фронтальной проекции фронтали, D2K2 ^ f2. 3. Вывод: К^Q(ΔABC)Þ[D2K2]^[A2B2C2]; [C1D1]^[A1B1C1]. Прямая линия, параллельная плоскости. Прямая параллельна плоскости, если она параллельна одной из прямых, лежащих в этой плоскости и не принадлежит этой плоскости. В общем случае, для решения задач на построение прямой, параллельно плоскости можно следовать этапам алгоритма, приведенным в табл. 5.2. Таблица 5.2
|



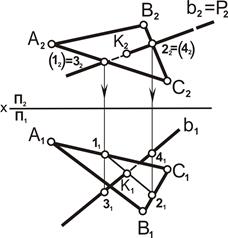
 Алгоритм построения.
Алгоритм построения. Прямая линия, перпендикулярная плоскости. Согласно элементарной геометрии, прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На заданной плоскости в качестве двух пересекающихся прямых целесообразно выбирать линии уровня – фронтали, горизонтали. В этом случае основанием решения будут являться свойства проецирования прямого угла.
Прямая линия, перпендикулярная плоскости. Согласно элементарной геометрии, прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости. На заданной плоскости в качестве двух пересекающихся прямых целесообразно выбирать линии уровня – фронтали, горизонтали. В этом случае основанием решения будут являться свойства проецирования прямого угла. Алгоритм построения перпендикуляра
Алгоритм построения перпендикуляра 


