| Словесная форма
| Графическая форма
|
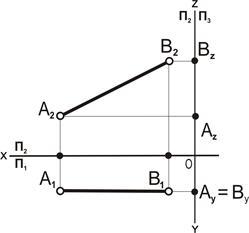
| 1. Отложить на осях координат x, y, z значение координат для точек А и В.
2. Построить проекции точек A и B:А1(x; –y), В1(x; –y), А2(x; z), В2 (x;z)
| 
|
| 3. Соединить одноименные проекции: А1 с В1, А2 с В2. Получим проекции отрезка АВ: [А1В1] и [А2В2]
| 
|
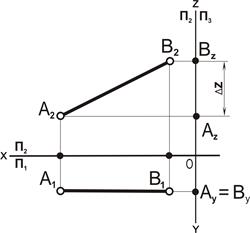
| 4. Определить ΔΖ и ΔY отрезка АВ:
ΔZ – это разность расстояний удаленности точек А и В до П1;
ΔΖ = Bz – Az = 65 – 15 = 50,
ΔY – это разность расстояний удаленности точек А и В от П2,
ΔY = By – Ay = 30 – 30 = 0
| 
|
Окончание табл. 4.2
| Словесная форма
| Графическая форма
|
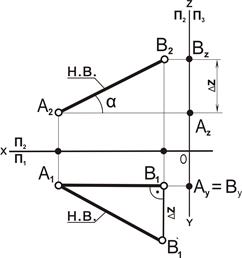
| 5. От точки В1 на перпендикуляре отложить Δz, |В1В`1|= ΔΖ
| 
|
| 6. Соединить точки А1 с В`1.
Отрезки А1 В`1 и А2В2 являются натуральной величиной отрезка АВ, так как (AB)|| П1, lАВl = |А`1 В1 | = |А`2В2|.
7. a – угол наклона отрезка АВ к плоскости П1
| 
|
Задача 2 б. Даны точки с координатами А(30; –85; 45), В(20; –40; 65).
1. По заданным координатам построить проекции отрезка в системе плоскостей П1П2.
Определить натуральную величину отрезка прямой линии и углы наклона к плоскостям проекций.
Алгоритм решения.
1. По данным координатам определить положение прямой линии относительно плоскостей проекций: отрезок прямой линии АВ занимает общее положение.
2. Применить алгоритм построения проекций отрезка прямой линии по координатам двух точек (табл. 4.3).
3. Применить метод прямоугольного треугольника для определения натуральной величины отрезка прямой линии АВ (табл. 4.3).
Таблица 4.3









