| Словесная форма
| Графическая форма
|
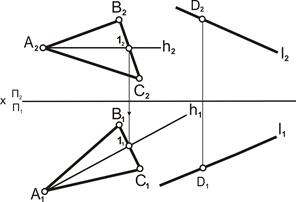
| 1. В плоскости Q(ΔАВС) построить горизонталь h:
– на фронтальной проекции треугольника провести прямую, параллельную оси OХ – фронтальную проекцию горизонтали, [h2]IIOX;
– в проекционной связи найти горизонтальную проекцию горизонтали
| 
|
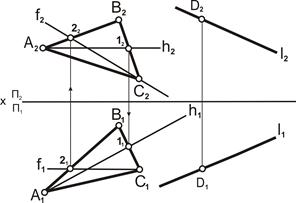
| 2. В плоскости Q(ΔАВС) построить фронталь f:
– на горизонтальной проекции треугольника провести прямую, параллельную оси ОХ, – горизонтальную проекцию фронтали, [f1]IIOX;
– в проекционной связи найти фронтальную проекцию фронтали
| 
|
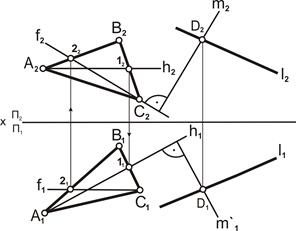
| 3. Через точку D на прямой l построить перпендикуляр к плоскости треугольника:
– на горизонтальной плоскости проекций построить перпендикуляр к горизонтальной проекции горизонтали, [m`1]^[h1];
– на фронтальной плоскости проекций построить перпендикуляр к фронтальной проекции фронтали, [m2]^[f2]
| 
|
Задача 7 б (варианты 13–18). Даныплоскость P(aIIb) и точка S (рис. 5.37).
Через точку S провести плоскость, параллельную данной.
Алгоритм решения.
1. Выполнить анализ данных условия задачи.
Выделить признаки, характеризующие понятие «плоскость», «плоскости параллельны» [18]; определить недостающие элементы чертежа, необходимые для выполнения условия параллельности плоскостей.
2. Составить план решения исходя и следующего:
– новую плоскость задать двумя пересекающимися прямыми;
– преобразовать способ задания плоскости данной так, чтобы она содержала прямые, пересекающиеся; определить, какие прямые, принадлежащие плоскости, построить можно всегда.
3. Выполнить построения (табл. 5.9).
Таблица 5.9
