Геометрические построения в примере

 

Словесная форма	Графическая форма
1. Построить горизонталь (либо фронталь) в плоскости Σ(ΔABC): – провести фронтальную проекцию горизонтали h2; – построить h1
2. Преобразовать плоскость треугольника общего положения (АВС) в проецирующую, повернув его вокруг осиi, АВС^П2: – провести осьi^П1 через вершину С, C1=i1; – горизонтальная проекция горизонтали h1 перпендикулярна оси Ох, h1^Ox, а A`1B`1C`1=A1B1C1; – на П2 треугольник проецируется в прямую линию A`2B`2
3. Преобразовать плоскость проецирующего треугольника А`В`С` в плоскость уровня, повернув его вокруг осиg, АВСII П1: – провести вторую ось g^П2 через вершину A`; – фронтальная проекция будет параллельна оси Ох; – горизонтальная проекция определяет натуральную величину треугольника:| |=IABCI

Метод плоскопараллельного перемещения. Плоскопараллельным перемещением фигуры в пространстве называется такое ее перемещение, при котором все точки фигуры перемещаются в параллельных плоскостях. В плоскопараллельном движении относительно плоскости П₁ все точки фигуры перемещаются в горизонтальных плоскостях, и горизонтальные проекции этих точек перемещаются, не изменяя своего взаимного положения. Фронтальная проекция тех же точек переходит в новые положения, двигаясь по прямым, перпендикулярным линиям связи. При плоскопараллельном движении относительно плоскости П₂ происходят аналогичные перемещения проекций. Плоскопараллельное перемещение может рассматриваться как вращение вокруг некоторой оси, перпендикулярной плоскости проекций и не показанной на чертеже.

Задача 6.5. Дан отрезок прямой линии общего положения АВ.

Преобразовать прямую линию
общего положения в линию уровня (рис. 6.7).

Алгоритм решения.

1. Расположить новую фронтальную проекцию [A`<sub>2</sub>B`₂] в любом месте эпюра перпендикулярно линиям связи, соблюдая условие, что |A`<sub>2</sub>B`₂| =
= |А₂В₂|.

2. Через заданную горизонтальную проекцию [А₁В₁] провести прямые, перпендикулярные линиям связи, и найти точки их пересечения с линиями связи, проведенными из точек [A`<sub>2</sub>B`₂].

Вывод. горизонтальной проекцией отрезка [АВ] будет являться отрезок [A`<sub>1</sub>B`₁], равный натуральной величине отрезка [АВ],| А`<sub>1</sub>B`₁I=IABI; b величина угла наклона заданной прямой АВ к плоскости П₂.

 

Задача 6.6. Преобразовать линию уров­­ня в проецирующую прямую
(рис. 6.8).

Дан отрезок прямой линии уровня АВ (горизонталь).

Алгоритм решения:

1. Переместить проекции [A^'₁B^'₁] в положение, параллельное вертикальным линиям связи, [A^'₁B^'₁ ]^(Ох), |A^'₁B^'₁| = IABI.

2. На пересечении линий связи от А₂В₂ и [A^'₁B^'₁] найти [A^'₂B^'₂].

Вывод. отрезок прямая уровня АВ методом плоскопараллельного перемещения преобразовалась во фронтально проецирующую прямую.

Для того чтобы прямую линию общего положения преобразовать
в проецирующую, необходимо выполнить два последовательных перемещения. Вначале прямую следует преобразовать в линию уровня
(рис. 6.7), а затем линию уровня преобразовать в проецирующую (рис. 6.8).

Задача 6.7. Дана плоскость общего положения Р(АВС).

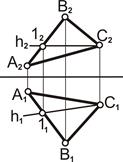
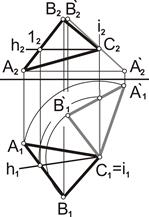
Преобразовать плоскости общего положения в проецирующую (рис. 6.9).

Алгоритм решения.

1. Построить горизонталь в плос­­кости Р(АВС), h (h₁, h₂).

2. Переместить горизонтальную проек­цию плоскости А`<sub>1</sub>В`₁С`<sub>1</sub> в вертикальное положение так, чтобы прямая h`₁ оказалась перпендикулярна оси Ох, А₁В₁С₁ =А`<sub>1</sub>В`₁С`<sub>1</sub>, h`₁^Ox.

3. Провести линии проекционной связи из точек А₂, В₂, С₂, А`<sub>1</sub>, В`₁, С`<sub>1</sub> на пересечении соответствующих проекций точек линии А`₂В`<sub>2</sub>С`₂.

Вывод. плоскость Р(АВС) методом плоскопараллельного перемещения преобразовалась во фронтально проецирующую плоскость, Р(АВС)^П₂.

Задача 6.8. Дана фронтально проецирующая плоскость Σ(АВС).

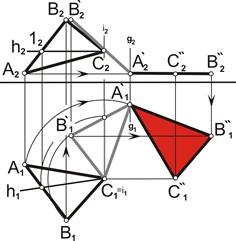
Преобразовать проецирующую плос­кость в плоскость уровня (рис. 6.10).

Алгоритм решения.

1. Переместить проекцию A₂B₂C₂
так, чтобы она оказалась параллельной оси проекций Ох. Получим проекцию A`<sub>2</sub>B`₂C`₂II Ох.

2. Провести линии проекционной связи от горизонтальных проекций точек А₁, В₁, С₁. Провести вспомогательные линии на П₁ от точек A`<sub>2</sub>B`₂C`<sub>2</sub>. На пересечении линий связи и вспомогательных линий от одноименных точек получим точки A`₁B`<sub>1</sub>C`₁.

Вывод. плоскость Σ(АВС) методом плоскопараллельного перемещения преобразовалась в горизонтальную плоскость уровня, Σ(АВС)IIП₁.

Для того чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо выполнить два последовательных перемещения. Вначале плоскость следует преобразовать в проецирующую (рис. 6.9), а затем проецирующую плоскость преобразовать в плоскость уровня (рис. 6.10).

Метод вращения вокруг линии уровня. Метод вращения вокруг линии уровня используется для определения натуральных величин элементов плоских фигур в тех случаях, когда плоскую фигуру можно совместить с плоскостью уровня. В этом случае она проецируется на соответствующую плоскость без искажения. Кроме того, этот метод удобен для определения углов между двумя пересекающимися прямыми, двумя плоскостями, прямой и плоскостью.

Рассмотрим вращение точки вокруг линии уровня (рис. 6.11). Точка А, вращаясь вокруг горизонтали h, описывает окружность радиусом, равным натуральной величине отрезка АО, O₁A`₁=IAOI, который можно определить методом прямоугольного треугольника. Аналогичным образом можно выполнить построения, вращая точку А вокруг фронтали.