Присутствие случайных ошибок в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных.
E — случайная величина (возмущение), характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии. Присутствие случайных ошибок в модели порождено тремя источниками: спецификацией модели, выборочным характером исходных данных, особенностями измерения переменных. a К ошибкам спецификации будут относиться: неправильный выбор той или иной математической функции для yтx, недоучет в уравнении регрессии какого-либо существенного фактора, например, использование парной регрессии вместо множественной. a Ошибки выборки имеют место и в силу неоднородности данных в исходной статистической совокупности, что, как правило, бывает при изучении экономических процессов. Если совокупность неоднородна, то уравнение регрессии не имеет практического смысла. Для получения хорошего результата обычно исключают из совокупности единицы с аномальными значениями исследуемых признаков. И в этом случае результаты регрессии представляют собой выборочные характеристики. Использование временной информации также представляет собой выборку из всего множества хронологических дат. Изменив временной интервал, можно получить другие результаты регрессии. a Наибольшую опасность в практическом использовании методов регрессии представляют ошибки измерения. Особенно велика роль ошибок измерения при исследовании на макроуровне. Предполагая, что ошибки измерения сведены к минимуму, основное внимание в эконометрических исследованиях уделяется ошибкам спецификации модели. В парной регрессии выбор вида математической функции yтx.=f(х) может быть осуществлен тремя методами: ¨ графическим; ¨ аналитическим, т. е. исходя из теории изучаемой взаимосвязи; ¨ экспериментальным. Графический метод подбора вида уравнения регрессии достаточно нагляден. Он основан на поле корреляции. Основные типы кривых, используемые при количественной оценке связей, представлены на рис.
Значительный интерес представляет аналитический метод выбора типа уравнения регрессии. Он основан на изучении материальной природы связи исследуемых признаков. Пример: изучается потребность предприятия в электроэнергии у в зависимости от объема выпускаемой продукции х. Все потребление электроэнергии у можно подразделить на две части: •не связанное с производством продукции а; •непосредственно связанное с объемом выпускаемой продукции, пропорционально возрастающее с увеличением объема выпуска (b• х). Тогда зависимость потребления электроэнергии от объема продукции можно выразить уравнением регрессии вида: yxТ=a+bx. Если затем разделить обе части уравнения на величину объема выпуска продукции (x), то получим выражение зависимости удельного расхода электроэнергии на единицу продукции от объёма выпущенной продукции (x) в виде уравнения равносторонней гиперболы: zxТ=b+a/x. При обработке информации на компьютере выбор вида уравнения регрессии осуществляется экспериментальным методом, т.е. путем сравнения величины остаточной дисперсии Dост, рассчитанной при разных моделях. Если уравнение регрессии проходит через все точки корреляционного поля, что возможно только при функциональной связи, когда все точки лежат на линии регрессии yтx.=f(х), то фактические значения результативного признака совпадают с теоретическими y=yтx., т. е. они полностью обусловлены влиянием фактора х. В этом случае остаточная дисперсия Dост. =0 В практических исследованиях, как правило, имеет место некоторое рассеяние точек относительно линии регрессии. Оно обусловлено влиянием прочих не учитываемых в уравнении регрессии факторов. Иными словами, имеют место отклонения фактических данных от теоретических (y - yтx.). Величина этих отклонений и лежит в основе расчета остаточной дисперсии: Dост.= Чем меньше величина Dост, тем меньше влияние прочих не учитываемых в уравнении регрессии факторов, тем лучше уравнение регрессии подходит к исходным данным. В автоматическом режиме выбирается математическая функция с наименьшей остаточной дисперсией. Если остаточная дисперсия оказывается примерно одинаковой для нескольких функций, то на практике предпочтение отдаётся более простым видам функций, т.к. они в большей степени поддаются интерпретации и требуют меньшего объёма наблюдений. (Известно, что число наблюдений должно 6-7 раз ревышать число расcчитываемых параметров при переменной x. Например, если мы выбираем параболу второй степени yТx=a+bx+cx2,то требуется объём информации уже не менее 14 наблюдений.)
2.1.Линейная регрессия и корреляция: смысл и оценка параметров. Линейная регрессия находит широкое применение в эконометрике в виде четкой экономической интерпретации ее параметров. Линейная регрессия сводится к нахождению уравнения вида: y=a+bx+E или yТx=a+bx – позволяет по заданным фактическим значениям фактора x иметь теоретические значения результативного признака. На графике теоретические значения представляют линию регрессии (см. рис.):
Построение линейной регрессии сводится к оценке ее параметров — а и b. Оценки параметров линейной регрессии могут быть найдены разными методами: 1.) можно обратиться к полю корреляции и, выбрав на графике две точки, провести через них прямую линию (см. рис.). Далее по графику можно определить значения параметров. Параметр а определим как точку пересечения линии регрессии с осью оу, а параметр b оценим, исходя из угла наклона линии регрессии, как b=tga=dy/dx, где dy — приращение результата y, а dx — приращение фактора х. 2.) Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК). МНК позволяет получить такие оценки параметров а и b при которых сумма квадратов отклонений фактических значений результативного признака у от расчетных (теоретических) yТx минимальна:
Т.е., из всего множества линий линия регрессии на графике выбирается так, чтобы сумма квадратов расстояний по вертикали между точками и этой линией была бы минимальной (см. рис.- линия регрессии с минимальной дисперсией остатков):
Чтобы найти минимум функции  надо вычислить частные производные по каждому из параметров a и b и прировнять их к нулю: надо вычислить частные производные по каждому из параметров a и b и прировнять их к нулю:
Преобразуя формулы, получим следующую систему нормальных уравнений для оценки параметров аи b:
Решая систему нормальных уравнений либо методом последовательного исключения переменных, либо методом определителей, найдем искомые оценки параметров а и b. Можно воспользоваться следующими готовыми формулами:
Параметр b называется коэффициентом регрессии. Его величина показывает среднее изменение результата с изменением фактора на одну единицу. Возможность четкой экономической интерпретации коэффициента регрессии сделала линейное уравнение регрессии достаточно распространенным в эконометрических исследованиях. Формально а — значение у при х = 0. Если признак-фактор х не имеет и не может иметь нулевого значения, то вышеуказанная трактовка свободного члена а не имеет смысла. параметр а может не иметь экономического содержания. Попытки экономически интерпретировать параметр а могут привести к абсурду, особенно при а < 0. Интерпретировать можно лишь знак при параметре а. Если а > 0, то относительное изменение результата происходит медленнее, чем изменение фактора.,т.е. вариация результата меньше вариации фактора - коэффициент вариации по фактору хвыше коэффициента вариации для результата у: Vx >Vy . Где
Если переменные х и у выразить через отклонения от средних уровней, то линия регрессии на графике пройдет через начало координат: y’т=bx’ где Оценка коэффициента регрессии при этом не изменится. Оценку коэффициента регрессии можно получить проще, не обращаясь к методу наименьших квадратов. Альтернативную оценку параметра b можно найти исходя из содержания данного коэффициента: изменение результата
Эта величина является приближенной, ибо большая часть информации, имеющейся в данных, не используется при ее расчете. Она основана только на минимальных и максимальных значениях переменных. Уравнение регрессии всегда дополняется показателем тесноты связи. При использовании линейной регрессии в качестве такого показателя выступает линейный коэффициент корреляции rxy.. Некоторые формулы линейного коэффициента корреляции:
Линейный коэффициент корреляции находится в границах: -1≤rxy≤1. Если коэффициент регрессии b>0, то 0≤rxy≤1, при b<0, -1≤rxy≤0. Следует иметь в виду, что величина линейного коэффициента корреляции оценивает тесноту связи рассматриваемых признаков в ее линейной форме. Поэтому близость абсолютной величины линейного коэффициента корреляции к нулю еще не означает отсутствие связи между признаками. При иной спецификации модели связь между признаками может оказаться достаточно тесной. Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции rxy2, называемый коэффициентом детерминации. Коэффициент детерминации характеризует долю дисперсии результативного признака у, объясняемую регрессией, в общей дисперсиирезультативного признака:
Величина коэффициента детерминации служит одним из критериев оценки качества линейной модели. Чем больше доля объясненной вариации, тем соответственно меньше роль прочих факторов, и, следовательно, линейная модель хорошо аппроксимирует исходные данные и ею можно воспользоваться для прогноза значений результативного признака. Соответственно величина 1-r2 характеризует долю дисперсии у, вызванную влиянием остальных не учтенных в модели факторов.
2.2. ОЦЕНКА СУЩЕСТВЕННОСТИ ПАРАМЕТРОВ
После того как найдено уравнение линейной регрессии, проводится оценка значимости как уравнения в целом, так и отдельных его параметров.
|



 . Т.к.
. Т.к.  ,то
,то 



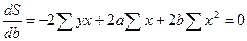

 (эта формула получена путём деления первого уравнения системы на n).
(эта формула получена путём деления первого уравнения системы на n). , где
, где  - ковариация признаков;
- ковариация признаков; - дисперсия признака x.
- дисперсия признака x. .
. - коэффициент вариации по x;
- коэффициент вариации по x; - среднеквадратическое отклонение x;
- среднеквадратическое отклонение x;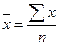 - среднеарифметическое отклонение x.
- среднеарифметическое отклонение x. и
и  .
. сопоставляют с изменением фактора
сопоставляют с изменением фактора 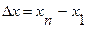 .
.

 .
.


