Доверительный интервал для коэффициента регрессии определяется как b±t mb.
Поскольку коэффициент регрессии в эконометрических. исследованиях имеет четкую экономическую интерпретацию, то доверительные границы интервала для коэффициента регрессии не должны содержать противоречивых результатов, например, -10 < b < 40. Такого рода запись указывает, что истинное значение коэффициента регрессии одновременно содержит положительные и отрицательные величины и даже ноль, чего не может быть. gСтандартная ошибка параметра а определяется по формуле:
Процедура оценивания существенности данного параметра не отличается от рассмотренной выше для коэффициента регрессии: вычисляется t-критерий: Значимость линейного коэффициента корреляции проверяется на основе величины ошибки коэффициента корреляции mr:
Фактическое значение t-критерия Стьюдента определяется как Данная формула свидетельствует, что в парной линейной регрессии tr2=F, так как Таким образом, проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии. Рассмотренная формула оценки коэффициента корреляции рекомендуется к применению при большом числе наблюдений и если r не близко к + 1 или -1. Если же величина коэффициента корреляции близка к + 1, то распределение его оценок отличается от нормального или распределения Стьюдента, так как величина коэффициента корреляции ограничена значениями от -1 до +1. Чтобы обойти это затруднение, Р. Фишером было предложено для оценки существенности rввести вспомогательную величину z, связанную с коэффициентом корреляции следующим отношением:
При изменении r от -1 до +1 величина zизменяется от -¥ до +¥, что соответствует нормальному распределению. Математический анализ доказывает, что распределение величины zмало отличается от нормального даже при близких к единице значениях коэффициента корреляции. Стандартная ошибка величины zопределяется по формуле:
Величину z можно не рассчитывать, а воспользоваться готовыми таблицами z-преобразования, в которых приведены значения величины z для соответствующих значений r. Ввиду того, что zи rсвязаны между собой приведенным выше соотношением, можно вычислить критические значения r, соответствующие каждому из значений r. Таблицы критических значений r разработаны для уровней значимости 0,05 и 0,01 и соответствующего числа степеней свободы. Критические значения rпредполагают справедливость нулевой гипотезы, т. е. rмало отлично от нуля. Если фактическое значение коэффициента корреляции по абсолютной величине превышает табличное, то данное значение r считается существенным. Если же r оказывается меньше табличного, то фактическое значение rнесущественно.
|


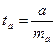 , его величина сравнивается с табличным значением при (п-2) степенях свободы.
, его величина сравнивается с табличным значением при (п-2) степенях свободы. .
.
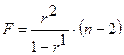 . Кроме того, tb2=F, следовательно tr2=tb2.
. Кроме того, tb2=F, следовательно tr2=tb2.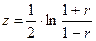
 где п — число наблюдений.
где п — число наблюдений.


