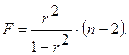Оценка значимости уравнения регрессии
Оценка значимости уравнения регрессии в целом дается с помощью критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент регрессии равен нулю, т. е. b= 0, и, следовательно, фактор х не оказывает влияния на результат у. Непосредственному расчету F-критерия предшествует дисперсионный. анализ Центральное место в нем занимает разложение обшей суммы квадратов отклонений переменной у от среднего значения
Общая сумма квадратов отклонений индивидуальных значений результативного признака у от среднего значения у вызвана влиянием множества причин. Условно разделим всю совокупность причин на две группы: изучаемый фактор х и прочие факторы. Если фактор не оказывает влияния на результат, то линия регрессии на графике параллельна оси ох и Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное воздействие на результат у. Это равносильно тому, что коэффициент детерминации rxy2будет приближаться к единице. Любая сумма квадратов отклонений связана с числом степеней свободы ( df — degrees of freedom), т. е. с числом свободы независимого варьирования признака. Число степеней свободы связано с числом единиц совокупности n ис числом определяемых по ней констант. Число степеней свободы показывает, сколько независимых отклонений из п возможных · Так, для общей суммы квадратов · При расчете объясненной или факторной суммы квадратов · Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Число степеней свободы остаточной суммы квадратов при линейной регрессии составляет dfост=n- 2. Итак, имеем два равенства:
Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, что то же самое, дисперсию на одну степень свободы:
Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя факторную и остаточную дисперсии в расчете на одну степень свободы, получим величину F-отношения (F-критерий):
Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга. Для Ho необходимо опровержение, чтобы факторная дисперсия превышала остаточную в несколько раз. Английским статистиком Снедекором разработаны таблицы критических значений F-отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия — это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности наличия нулевой гипотезы. Вычисленное значение F-отношения признается достоверным (отличным от единицы), если оно больше табличного. В этом случае нулевая гипотеза об отсутствии связи признаков отклоняется и делается вывод о существенности этой связи: Fфакт>FтаблÞHo отклоняется. Если же величина окажется меньше табличной Fфакт<Fтабл, то вероятность нулевой гипотезы выше заданного уровня (например, 0,05) и она не может быть отклонена без серьезного риска сделать неправильный вывод о наличии связи. В этом случае уравнение регрессии считается статистически незначимым. Ho не отклоняется.
Величина F-критерия связана с коэффициентом детерминации r2. Факторную сумму квадратов отклонений можно представить как
|

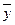 на две части — «объясненную» и «необъясненную»:
на две части — «объясненную» и «необъясненную»: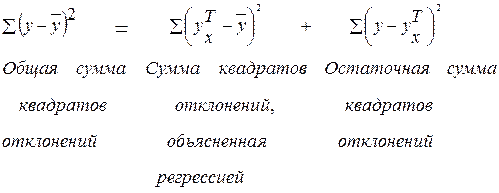
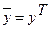 . Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.
. Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма квадратов отклонений совпадет с остаточной. Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю. В этом случае сумма квадратов отклонений, объясненная регрессией, совпадает с общей суммой квадратов.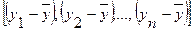 требуется для образования данной суммы квадратов.
требуется для образования данной суммы квадратов.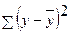 требуется (п - 1) независимых отклонений, т.к. из п единиц после расчета среднего уровня свободно варьируют лишь (п — 1) число отклонений. Например, имеем ряд значений y: 1, 2, 3, 4, 5. Среднее из них равно 3, и тогда п отклонений от среднего составят: -2; - 1; 0; 1; 2. Так как
требуется (п - 1) независимых отклонений, т.к. из п единиц после расчета среднего уровня свободно варьируют лишь (п — 1) число отклонений. Например, имеем ряд значений y: 1, 2, 3, 4, 5. Среднее из них равно 3, и тогда п отклонений от среднего составят: -2; - 1; 0; 1; 2. Так как 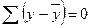 , то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если предыдущие четыре известны. Итак, dfобщ=n-1.
, то свободно варьируют лишь четыре отклонения, а пятое отклонение может быть определено, если предыдущие четыре известны. Итак, dfобщ=n-1.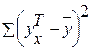 используются теоретические (расчетные) значения результативного признака уxТ, найденные по линии регрессии: уxТ = а +b х. Очевидно, что
используются теоретические (расчетные) значения результативного признака уxТ, найденные по линии регрессии: уxТ = а +b х. Очевидно, что 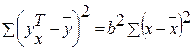 . Поскольку при заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы: dfобъясн. регр.=1.
. Поскольку при заданном объеме наблюдений по х и у факторная сумма квадратов при линейной регрессии зависит только от одной константы коэффициента регрессии b, то данная сумма квадратов имеет одну степень свободы: dfобъясн. регр.=1.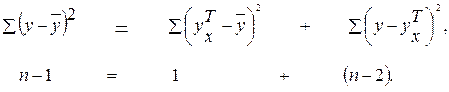
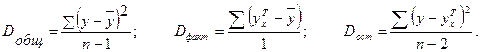
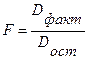 , где F-критерий для проверки нулевой гипотезы Ho: Dфакт=Dост.
, где F-критерий для проверки нулевой гипотезы Ho: Dфакт=Dост.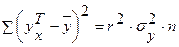 , а остаточную сумму квадратов
, а остаточную сумму квадратов  — как
— как 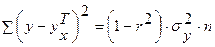 . Тогда значение F-критерия можно выразить как
. Тогда значение F-критерия можно выразить как