ИНТЕРВАЛЫ ПРОГНОЗА
В прогнозных расчетах по уравнению регрессии определяется предсказываемое уp значение как точечный прогноз теоретического значения yxT при xp=xk: уp=а+b хp. Однако точечный прогноз явно не реален. Поэтому он дополняется расчетом стандартной ошибки уxТ, - myp,и интервальной оценки прогнозного значения – строится доверительный интервал прогноза. Выведём формулу для myp. Имеем уравнение линейной регрессии: уxT=а+bх.Подставим в это уравнение выражение параметра а: Следовательно, стандартная ошибка myp зависит от ошибки Из теории выборки известно, что Ошибка коэффициента регрессии, как уже было показано, определяется формулой:
Соответственно myp имеет выражение: Интервальная оценка прогнозного значения (у*):
Рассмотренная формула стандартной ошибки предсказываемого среднего значения у при заданном значении xk характеризует ошибку положения линии регрессии. Величина стандартной ошибки Для прогнозируемого значения
На графике доверительные границы для Рис. показывает, как изменяются пределы в зависимости от изменения xk: a – верхняя доверительная граница; б – линия регрессии; в – доверительный интервал для
Рис. Доверительный интервал линии регрессии. Две гиперболы по обе стороны от линии регрессии определяют 95%-ные доверительные интервалы для среднего значения у при заданном значении х. Однако фактические значения у варьируют около среднего значения Средняя ошибка прогнозируемого индивидуального значения у
При прогнозировании на оcнове уравнения регрессии следует помнить, что величина прогноза зависит не только от стандартной ошибки индивидуального значения у, но и от точности прогноза значения фактора х. Его величина может задаваться на основе анализа других моделей исходя из конкретной ситуации, а также из анализа динамики данного фактора. Рассмотренная формула средней ошибки индивидуального значения
|

 , тогда уравнение регрессии примет вид:
, тогда уравнение регрессии примет вид: 
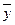 и ошибки коэффициента регрессии b, т.е.
и ошибки коэффициента регрессии b, т.е. 
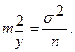 Используя в качестве оценки σ2 остаточную дисперсию на одну степень свободы Dост (
Используя в качестве оценки σ2 остаточную дисперсию на одну степень свободы Dост ( ), получим формулу расчета ошибки среднего значения переменной у:
), получим формулу расчета ошибки среднего значения переменной у: 
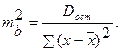 Считая, что прогнозное значение фактора xp=xk, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения:
Считая, что прогнозное значение фактора xp=xk, получим следующую формулу расчета стандартной ошибки предсказываемого по линии регрессии значения:

 -
- 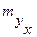
 y*
y*  и возрастает по мере того, как удаляется от
и возрастает по мере того, как удаляется от  в любом направлении. Иными словами, чем больше разность между xk и
в любом направлении. Иными словами, чем больше разность между xk и 
 tα*
tα* 
 .
. составит:
составит:



