Корреляция для нелинейной регрессии
Уравнение линейной регрессии дополняется показателем корреляции – индексом корреляции.
Величина R находится в границах: 0≤ R ≤ 1, чем ближе к единице, тем связь рассмотренных признаков теснее – тем более надёжно найденное уравнение регрессии. 1)если преобразования уравнения в линейную форму связаны с независимой переменной (х), то для оценки тесноты связи может быть использован линейный коэффициент корреляции, так как его величина совпадает с индексом корреляции.
Ryx=ryz, где z может быть z=lg x, ln x, 1/x Данное утверждение справедливо для равносторонней гиперболы, полулогарифмической кривой. 2)если преобразования в линейную форму связаны с зависимой переменной (у), то используемый коэффициент корреляции по преобразованным значениям признаков даёт приближённую оценку тесноты связи и численно не совпадает с индексом корреляции.
Ryx ≠rxz, где z – преобразованная переменная y Оценка существенности R проводится аналогично оценке надёжности коэффициента корреляции (см. предыдущий материал, а именно п.2.2). Индекс детерминации используется для проверки качества уравнения нелинейной регрессии. Для оценки статистической значимости уравнения нелинейной регрессии рассчитывают F- критерий Фишера, и сравнивают его с табличным значением.
где R2 – коэффициент детерминации, n – число наблюдений, m – число параметров при переменной х.
|
- общая дисперсия результативного признака y;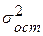
- остаточная дисперсия, определяемая из уравнения дисперсии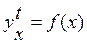 
,
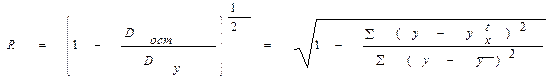
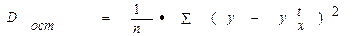
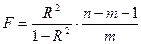