Фактические значения результативного признака отличаются от теоретических, рассчитанных по уравнению регрессии, т. е. y и  . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у-
. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у-  ) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует обьему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у-
) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует обьему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у-  х) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения у-
х) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения у-  =5, а для другого она равна 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений. Выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у = 20, а для второго у = 50, ошибка аппроксимации составит 25% для первого наблюдения и 20% - для второго.
=5, а для другого она равна 10, то это не означает, что во втором случае модель дает вдвое худший результат. Для сравнения используются величины отклонений. Выраженные в процентах к фактическим значениям. Так, если для первого наблюдения у = 20, а для второго у = 50, ошибка аппроксимации составит 25% для первого наблюдения и 20% - для второго.
Поскольку (у-  ) может быть величиной как положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
) может быть величиной как положительной, так и отрицательной, то ошибки аппроксимации для каждого наблюдения принято определять в процентах по модулю.
Отклонение (у-  ) можно рассматривать как абсолютную ошибку аппроксимации, а
) можно рассматривать как абсолютную ошибку аппроксимации, а  *100 - как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
*100 - как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
А = 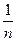 *
*  *100.
*100.
Возможно и иное определение средней ошибки аппроксимации:
А =  *
* 
В стандартных программах чаще используется первая формула для расчета средней ошибки аппроксимации.

 . Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у-
. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, лучше качество модели. Величина отклонений фактических и расчетных значений результативного признака (у-  ) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует обьему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у-
) по каждому наблюдению представляет собой ошибку аппроксимации. Их число соответствует обьему совокупности. В отдельных случаях ошибка аппроксимации может оказаться равной нулю. Отклонения (у-  х) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения у-
х) несравнимы между собой, исключая величину, равную нулю. Так, если для одного наблюдения у-  *100 - как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую:
*100 - как относительную ошибку аппроксимации. Чтобы иметь общее суждение о качестве модели из относительных отклонений по каждому наблюдению, определяют среднюю ошибку аппроксимации как среднюю арифметическую простую: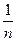 *
*  *100.
*100. *
* 



