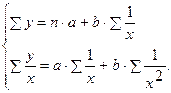I. Регрессии, нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам.
Примером могут служить следующие функции: 1) полиномы разных степеней — y=a+bx+cx2+E, y=a+bx+cx2+dx3+E, и т.д.; 2) равносторонняя гипербола — y=a+b/x+E; 3) полулогарифмическая кривая — y=a+b lnx+E; 4) кривые, задающиеся уравнениями с квадратными корнями — y=a+b√x+E; и другие функции. Оценка ее параметров нелинейной регрессии по включенным переменным определяется, как и в линейной регрессии, методом наименьших квадратов (МНК), так как эти функции линейны по параметрам. 1) Для полинома второго порядка: y=a0+a1x+a2x2+E заменим x=x1, x2=x1, получим y=a0+a1x1+a2x2+E – двухфакторное уравнение линейной регрессии. Для полинома третьего порядка: y=a0+a1x+a2x2+a3x3+E заменим x=x1, x2=x1, x3=x3, получим y=a0+a1x1+a2x2+a3x3+E – трёхфакторное уравнение линейной регрессии. Для полинома k-го порядка: y=a0+a1x+a2x2+…+akxk+E заменим x=x1, x2=x1,…, xk=xk, получим y=a0+a1x1+a2x2+…+akxk+E – уравнение множественной линейной регрессии с k объясняющими переменными. Итак, полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени; в отдельных случаях — полином третьего порядка. (Ограничения в использовании полиномов более высоких степеней связаны с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и соответственно менее однородна совокупность по результативному признаку.) Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи рассматриваемых признаков: прямая связь меняется на обратную или обратная на прямую. В этом случае определяется значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака: приравниваем к нулю первую производную параболы второй степени: yхT=a+bх+сх2, y’=b+2сх=0 и х= - b/2c. Если же исходные данные не обнаруживают изменения направленности связи, то параметры параболы второго порядка становятся трудно интерпретируемыми, а форма связи часто заменяется другими нелинейными моделями. Рассмотрим метод оценивания параметров параболы второй степени - МНК, который приводит к следующей системе нормальных уравнений:
Решить её можно, например, методом определителей:
При b>0 и c<0 кривая симметрична относительно высшей точки, т.е. точки перелома кривой, изменяющей направление связи, а именно рост на падение.Если параболическая форма связи демонстрирует сначала рост, а затем снижение уровня значений результативного признака, то определяется значение фактора, при котором достигается максимум. При b<0 и с>0 парабола второго порядка симметрична относительно своей низшей точки, что позволяет определять минимум функции в точке, меняющей направление связи, т. е. снижение на рост. Ввиду симметричности кривой парабола второй степени далеко не всегда пригодна в конкретных исследованиях. Чаще исследователь имеет дело лишь с отдельными сегментами параболы, а не с полной параболической формой. Кроме того, параметры параболической связи не всегда могут быть логически истолкованы. Поэтому если график зависимости не демонстрирует четко выраженной параболы второго порядка (нет смены направленности связи признаков), то она может быть заменена другой нелинейной функцией, например степенной.
2) Рассмотрим равностороннюю гиперболу: у=a+b/x+E. Её параметры также оцениваются методом наименьших квадратов. Заменив 1/x=z, получим линейное уравнение регрессии у=а+bz+E, оценка параметров которого может быть дана МНК. Система нормальных уравнений составит:
При b>0 имеем обратную зависимость, которая при x→∞, характеризуется нижней асимптотой, т. е. минимальным предельным значением у, оценкой которого служит параметр a. При Ь < 0 имеем медленно повышающуюся функцию с верхней асимптотой при x→∞, т. е. с максимальным предельным уровнем у, оценку которого в уравнении даёт параметр a. 3) Рассмотрим полулогарифмическую кривую: y=a+b lnx+E. Заменив lnx=z опять получим линейное уравнение y=a+b z+E. Данная функция, как и предыдущая, линейна по параметрам и нелинейна по объясняющей переменной х. Оценка параметров a и b быть найдена МНК. Система нормальных уравнений при этом окажется следующей:
4) Для уравнений с квадратными корнями у = а+b√х+Е система нормальных уравнений для оценки параметров составит:
Уравнения с квадратными корнями использовались в исследованиях урожайности, трудоемкости сельскохозяйственного производства
|

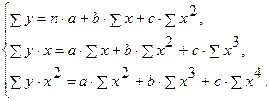
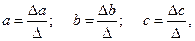 где Δ – определитель системы; Δa,Δb,Δc – частные определители для каждого из параметоров.
где Δ – определитель системы; Δa,Δb,Δc – частные определители для каждого из параметоров.