II. Регрессии, нелинейные по оцениваемым параметрам.
Данный класс нелинейных моделей подразделяется на два типа: II.а) нелинейные модели внутренне нелинейные (нелинейная модель внутренне нелинейна если она не может быть сведена к линейной функции). К таким моделям можно отнести: Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях., но мы будем рассматривать лишь внутренне линейные модели. II.б) нелинейные модели внутренне линейные (нелинейная модель внутренне линейна если она может быть сведена к линейной функции); Эти модели получили гораздо большее распространение, к ним можно отнести: 1) степенная — y=a xb E; 2) показательная — y=a bx E; 3) экспоненциальная — y=ea+bx E; 4) обратная — 5) логистическая — Такие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. Рассмотрим на примере экспоненциальной модели y=ea+bxE процесс её линеаризации: логарифмируя ее по натуральному основанию, получим линейную форму модели: Lny=a+b x+lnE. Аналогичным образом, путем логарифмирования, приводят к линейному виду степенную и показательную функции. Линеаризация для обратной модели происходит путём обращения обеих частей равенства Приводима к линейному виду и логистическая функция: Преобразовывая равенство, получим:
Обозначив, В эконометрике широко используются коэффициенты эластичности. Формула расчета коэффициента эластичности: где f’(x) – первая производная, характеризующая соотношение приростов результата и фактора для соответствующей модели. Из данной формулы видно, что коэффициент эластичности показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%. Приведем формулы расчета коэффициентов эластичности для наиболее распространенных типов уравнений регрессии:
В силу того, что коэффициент эластичности для степенной функции является величиной постоянной, равной параметру b, а у других форм связи коэффициент эластичности зависит от значений фактора x, то в эконометрических исследованиях очень широко используется степенная функция y=axbE (в ней параметр b имеет чёткое экономическое истолкование). Так как коэффициент эластичности для линейной функции не является величиной постоянной, а зависит от соответствующего значения х, то обычно рассчитывается средний показатель эластичности по формуле: Несмотря на широкое использование в эконометрике коэффициентов эластичности, возможны случаи, когда их расчет экономического смысла не имеет. Это происходит тогда, когда для рассматриваемых признаков бессмысленно определение изменения значений в процентах.
|

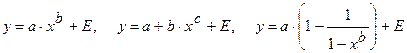 , так как эти уравнения не могут быть преобразованы в уравнения линейные по коэффициентам.
, так как эти уравнения не могут быть преобразованы в уравнения линейные по коэффициентам.
 и другие.
и другие.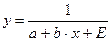 . Так получим линейную форму модели для переменной
. Так получим линейную форму модели для переменной  .
. .
.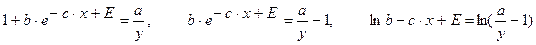 .
. , имеем:
, имеем:  .
. ,
,









 .
.


