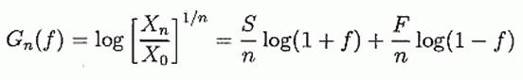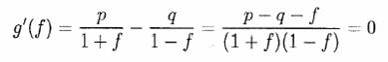Подбрасывание монеты

Допустим, мы играем с бесконечно богатым противником, который будет делать повторяющиеся ставки на независимые события – броски монеты. Далее, предположим, что при каждом броске наша вероятность победы p> 1/2, а вероятность потери q = 1 - p. Наш начальный капитал - X_O. Предположим, что наша цель – максимизация ожидаемой величины E (X_n) через n попыток. Сколько мы поставим, B_{k ,} на k -ой попытке? Пусть T_k = 1, если k -я попытка - выигрышная и T_k = -1, если она проиграна, тогда X_k =X_k-1 + T_k B_k для k = 1,2,3.., и X_n = X_O + Σ;ⁿ_k=1T_kB_k. Тогда

Так как игра имеет положительное ожидание, то есть p-q> 0, в этой ситуации равных выплат, для того, чтобы максимизировать Е(Х_n), мы должны были бы максимизировать E(B_k) для каждой попытки. Таким образом, чтобы максимизировать ожидаемый рост мы должны ставить все наши ресурсы в каждой попытке. Таким образом, B₁ = X₀, и, если мы выигрываем первую ставку, B₂ = 2X₀, и т.д. Однако, вероятность краха при этом будет 1 - p^N и при p < 1, lim _n→∞ [1 —рⁿ] = 1, так что крах почти неизбежен. Таким образом, "смелый" критерий ставок для максимизации ожидаемого роста обычно нежелателен.

Аналогично, если наша стратегия состоит в том, чтобы минимизировать вероятность возможного краха (а "крах" происходит, если X_K = 0 на k-ой попытке) широко известная формула краха игрока (по Feller (1966)) показывает, что мы минимизируем крах, делая минимальную ставку на каждой попытке, но это, к сожалению, также минимизирует и ожидаемый рост. Таким образом, "робкая" система ставок также непривлекательна.

Это предполагает существование промежуточной стратегия, которая лежит где-то между максимизацией E (X_n) (и верным крахом) и уменьшением вероятности краха (и уменьшением E (Х_n)). Асимптотически оптимальная стратегия была впервые предложена J.L. Kelly (1956).

Так как вероятности и выплаты при каждой ставке в описанной игре с подбрасыванием монеты одинаковы, кажется вполне правдоподобно, что "оптимальная" стратегия потребует всегда держать пари на одну и ту же долю f вашего капитала. Чтобы это было возможным сделать, мы предполагаем далее, что капитал может бесконечно дробиться. Это предположение обычно не имеет большого значения в практическом применении.

Стратегия, в которой ставки делаются согласно B_i = f X_i-1, где 0 ≤ f ≤ 1, иногда называется стратегией "фиксированной доли". Пусть S и F - числа успехов и проигрышей в n попытках соответственно, тогда наш капитал после n попыток равен X_n = X_o(1+ f)^S (1-f)^F, где S + F = n. При f в интервале 0 < f < 1, Рr (Х_n = 0) = 0. Таким образом, "краха", понимаемом в техническом смысле как разорение игрока, произойти не может. "Крах" впредь будет означать, что для произвольно маленького положительного ε, lim_n→∞[Рr(X_n ≤ ε)] = 1. В этом смысле, как мы увидим, крах все-таки может случиться при некоторых обстоятельствах.

Отметим, что так как

величина

измеряет экспоненциальную скорость роста за попытку. Kelly максимизировал ожидаемую величину коэффициента скорости роста, g(f), где

 

Обратите внимание, что g(f) = (1/n)E[logX_n]- (1/n)logX₀, поэтому, для фиксированного n, максимизация g(f) - то же самое, что максимизация E[logX_n]. В дальнейшем обсуждении мы в основном будем говорить о максимизации g(f). Заметим, что

когда f = f ^* = p - q.

Так как

то g' (f) убывает строго монотонно на [0, 1), Так как g' (0) = p-q > 0 и lim _f→1 - g'(f) = - ∞. Вследствие непрерывности g'(f), g (f) имеет единственный максимум в точке f=f *, где g(f *) = p log p + q log q + log 2 > 0. Более того, поскольку g(0) = 0 и lim _f→1 - g{f) = - ∞, то существует единственное f_C >; 0, такое что 0 < f* < f_C < 1 и g(f_C) = 0. Природа функции g(f) теперь очевидна, и график g(f) от f выглядит так, как показано на Рисунке 1.

Следующая теорема излагает важные преимущества максимизации g(f). Детали здесь опущены, но доказательства (i), (ii), (iii), и (vi) для простого биномиального случая могут быть найдены в Thorp (1969); более общее доказательство этого, а также доказательства (iv) и (v) можно найти у Breiman (1961).

Теорема 1 (i) Если g(f) > 0, тогда почти достоверно, что lim_n→∞ Х_n = ∞;, то есть для каждого М, Pr [lim _n→∞ inf Х_n > М] = 1;

(ii) если g(f) < 0, тогда почти достоверно, что lim_n→∞ Х_n = 0, то есть для каждого ε>0, Pr [lim _n→∞ sup Х_n < ε] = 1;

(iii) Если g(f) = 0, тогда почти достоверно, что lim _n→∞ sup Х_n= ∞; и lim _n→∞ inf Х_n = 0.

(iv) Для заданной стратегии Ф*, которая максимизирует E[log X_n] и любой другой "существенно иной" стратегии Ф (не обязательно стратегии фиксированных дробных ставок) почти достоверно, что lim_n→∞ Х_n(Ф*)/Х_n (Ф) = ∞;.

(v) Ожидаемое время, необходимое чтобы текущий капитал X _n достиг заранее установленного значения С будет, асимптотически, наименьшим при стратегии, которая максимизирует E[log X_n].

(vi) Предположим, что отдача от одной ставки на i-ой попытке - биноминальная случайная переменная U_i, далее предположим, что вероятность успеха p _i, где 1/2 < p_i < 1. Тогда E[log X_n] максимизируется выбором значением для ставки при каждой попытке доли f *_i = p_i - q_i которая максимизирует E[ log (1+f_iU_i)].

Часть (i) показывает что, если бы не конечное время, благосостояние игрока X_N превысило бы любой установленный предел М, когда f выбрано в интервале (0, f _с). Но, если f > f _C, часть (ii) показывает, что крах почти неизбежен. Часть (iii) демонстрирует, что, если f = f _C, Х_n будет (почти достоверно) беспорядочно колебаться между 0 и + ∞;, Таким образом, утверждение одного из авторов, что X_n →; X₀ при n → ∞;, когда f = f_с, явно противоречиво. Части (iv) и (v), показывают, что стратегия Kelly максимизирования E[logX_n] является асимптотически оптимальной в соответствии с двумя важными критериями. "Существенно иная " стратегия - одна из таких, что разница E[ ln X_n*] – E[ lnX_n] между стратегией Kelly и другой стратегией растет быстрее, чем стандартное отклонение ln X_n* - ln X _n, обеспечивая Р (ln X_n* - ln X _n > 0) → 1. Часть (vi) устанавливает справедливость использования метода Kelly выбора f_i* при каждой попытке (даже если от одной попытки к следующей меняется вероятность) для максимизации E[log X_n].

Пример 2.1 Игрок А играет против бесконечно богатого противника. Игрок выигрывает одну и ту же сумму при последовательных независимых бросках монеты с вероятностью p =0,53 (независимые события). Игрок А имеет начальный капитал X₀, и капитал может бесконечно делиться. Применяя Теорему 1 (vi), f* = p - q = 0,53 – 0,47 = 0,06, Таким образом, в каждой игре он должен ставить 6 % текущего капитала,чтобы X_n рос с максимальной скоростью и с нулевой вероятностью краха. Если Игрок А постоянно ставит меньшую долю, чем 6 %, X_n также будет расти до бесконечности, но медленнее.

Если Игрок A постоянно ставит долей большей чем 6 %, но меньше f_с , возникает то же самое. Решая уравнение g(f) = 0,53log (l +f) + 0,47log (l - f) = 0 численно на компьютере получаем fc = 0,11973 ^¯. Так, если ставка больше чем примерно 12 %, то даже при том, что Игрок А может временно наслаждаться быстрой скоростью роста, возможные колебания вниз непременно приведут величину X_n к нулю. Вычисление дает коэффициент роста g(f*)= f (0,06) = 0,001801 так, что после n последовательных ставок логарифм среднего величины капитала Игрока А будет стремиться к значению в 0,001801*n раз превышающему стартовый капитал. Приравнивая 0,001801n = log 2, получаем ожидаемое время, необходимое для удвоения капитала примерно равное n = 385.

Критерий Кэлли может легко быть расширен на игры с неравными выплатами. Предположим, Игрок А выигрывает b единиц на каждую единицу ставки. Далее предположим, что на каждой попытке вероятность победы p>; 0 и pb - q> 0, так что игра выгодна для Игрока А. Методы, подобные рассмотренным, могут использоваться для максимизации

Вычисления дают f* = (bp - q)/b, оптимальную долю текущего капитала, которая должна быть поставлена в каждой игре, чтобы максимизировать коэффициент роста g (f).

Эта формула для f ^* появилась в Thorp (1984) и была предметом обсуждения в апреле 1997 в интернете на сайте Станфорда Вонга http://bj21.com. Один из обсуждавшихся там вопросов состоял в том, что можно потерять только равные по величине ставки, так что нет оснований рассматривать простое обобщение этой формулы для ситуации, когда единица ставки выигрывает b с вероятностью p> 0 и теряет a с вероятностью q. Тогда, если ожидание m ≡ bp - aq > 0, f* > 0 и f* = m/ab. Обобщение, однако, необходимо. Можно покупать в кредит на финансовых рынках и терять гораздо больше ставки. Примеры: покупка товарного фьючерса или короткая продажу (когда потеря потенциально неограничена). См., например, Thorp и Kassouf (1967).

Педанты, которые настаивают, что эти выплаты не биноминальны, могут рассмотреть короткую продажу способом двоичных чисел. Эти способы описаны у Browne (1996).

Критика, иногда звучащая в адрес стратегии Kelly – то, что капитал на самом деле не делится бесконечно. В реальном мире, ставки - умноженные минимальные единицы, типа 1 $ или 0,01 $. На рынках ценных бумаг, где система учета компьютеризованна, минимальная единица может быть сколь угодно малой. С учетом минимально позволенной ставки "крах" в обычном смысле возможен всегда. Не трудно показать, однако, (см. Thorp и Waiden, 1966) что, если минимальная позволенная ставка невелика относительно начального капитала игрока, то, вероятность краха в обычном смысле незначительна, а также то, что теория, описанная здесь, является полезной аппроксимацией. Этот раздел написан согласно работе Rotando and Thorp (1992).