Долгосрочный период: когда "доминирует" стратегия Келли?

Несколько позже John Leib написал несколько статей на форуме по Блэк джеку с критикой критерия Келли. Он был очень смущен "длинной дистанцией". Что это и когда оно происходит? Начнем с примера.

Пример 4.1p=0.51, n=10,000

V_i и s_i, i=1,2 дисперсия и стандартное отклонение, соответственно, для Случаев 1 и 2 из 3(е), а R=V₂/V₁ =(a² + b²)/(a-b)² так, что s₂=s₁√R. В Таблице 4.1 приведены некоторые результаты. Мы можем также аппроксимировать √R степенным рядом, используя лишь первые члены для a и b: a = 2f₁, b=2f₂ в виде

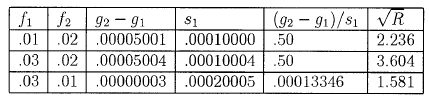
Приближенные результаты, которые очень близки к точным, будут, соответственно, 2.236, 3.606, и 1.581.

ТАБЛИЦА 4.1. Сравнение стратегий

Первые два ряда показывают, как почти симметрично поведение с каждой стороны оптимального f*=0.02. Колонка (g₂—g₁)/S₁ показывает нам, что при f* =.02 мы имеем преимущество перед соседями f = .01 и f=.03 после n =10,000 попыток только в размере 0.5 стандартных отклонений. Теперь, так как это преимущество пропорционально √n, колонка (g₂—g₁)/s₁ из Таблицы 4.1 дает результаты Таблицы 4.2:

ТАБЛИЦА 4.2 Долгосрочный пробег: (g₂—g₁)/ s после n попыток.

Фактор √R из Таблицы 4.1 показывает, насколько медленнее f ₂ достигает цели по сравнению с f ₁ в Случае 1 по сравнению со Случаем 2. Отношение (g₂—g₁)/S₂ в √R раз больше. Когда в реальном мире сравнивают стратегии, из практических соображений чаще для сравнения используют Случай 2 чем более подходящий Случай 1, превосходство f* в дальнейшем затеняется. Пример - игроки с различными долями ставок в блэк джеке. Случай 1 соответствует ставкам на той же самой последовательности сдач карт. Случай 2 выражает игру за разными столами (поэтому Случай 2 предполагает независимость). (Из-за положительной корреляции между выплат на сдачах, сыгранных за одним и тем же столом, это промежуточное состояние между Случаем 1 и Случаем 2.)

Важно понять, что "долгий срок ", то есть время, которое требуется, чтобы f * стало доминировать над соседними с указанной вероятностью, может меняться неограниченно. Каждое приложение требует отдельного анализа. В таких случаях, как в Примере 4.1, где доминанта - "медленная ", можно сказать, что использование f* - не существенно. В качестве аргумента против этого, рассмотрите два броска монеты. В игре 1 ваше преимущество - 1.0 %. В игре 2 - 1,1 %. При ставке, равной единице, после n попыток разница в ожидаемом росте будет Е₂ - Е₁ =0.001n со стандартным отклонением s около √2n, следовательно (Е₂ - Е₁)/s=0.001√n/√2, что составляет 1, когда n=2 * 10⁶, Так что требуется два миллиона попыток, чтобы иметь шанс в 84 % того, что результат игры 2 будет лучше, чем результат игры 1. Означает ли это несущественность выбора игры с более высоким ожиданием?