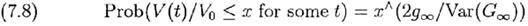Согласно (1) выбор f в диапазоне 0,5fe*£ f< fe* обеспечивает защиту от случая g£ 0 с уменьшением g, которое вероятно будет не более 25%.

Пример 7.3. Великий «сложнопроцентщик». В 1964 году молодой управляющий хедж-фонда приобрёл значительную долю в маленькой текстильной компании из Новой Англии под названием Berkshire Hathaway. Её акции торговались тогда по 20. В 1998 они торгуются по 70000, что в 3500 раз больше, а ежегодная ставка роста по сложному проценту составила около 27%, что равно 24%-ой мгновенной ставке. Некогда молодой управляющий хедж-фонда Warren Buffet – по общему признанию сейчас является величайшим инвестором нашего времени и обладателем вторым по величине состояния во всем мире. Вы можете прочитать о нем в (Buffet and Clarck,1997), Hagstrom (1994), Kilpatrick (1994) и Lowenstein (1995). Если бы вы были достаточно удачливы, как был я, чтобы повстречать Баффета и определить возможные перспективы компании Berkshire, какую стратегию предполагает использование нашего метода? Примем (что-то типа меньшего уровня смещений) m=0,20; s=0,15; r=0,6 (примечание: Правдоподобные аргументы в пользу малого значения смещений в будущем включают регрессия по направлению к среднему, увеличение размера компании Berkshire и возникающие риски из-за устаревания методов менеджмента. Контраргумент – сложнопроцентная ставка динамики роста компании в последние годы была также высока, как и раньше. Однако, индекс S&P 500 в последние годы показывает гораздо более высокие результаты, так что разрыв в величинах уровней роста индекса и Berkshire был несколько меньше. Таким образом, если мы ожидаем, что уровень роста индекса будет возвращаться по направлению к историческому среднему значению, тогда мы ожидаем того же самого поведения от Berkshire, даже в ещё большей степени.) Из уравнений (7.3) или (7.7),

Сравним это с безрычаговым портфелем, где f=1 и с=1/6,2(2)=0,1607.

Мы находим

Кредитное плечо здесь на уровне 6,2(2) будет нецелесообразным в реальности из-за того, что цены на бумаги могут меняться внезапно и прерывно. Во время краха в октябре 1987 года индекс S&P 500 упал на 23% за один день. Если это произошло при плече 2,0, новое значение плеча неожиданно становиться 77/27=2,85 перед перетряской портфеля путём продажи его части. В случае c Berkshire, где был большой хорошо диверсифицированный портфель, предположим, что мы выбираем консервативное значение f=2,0. Отметим, что это максимально возможное для «клиентов» при нынешних правилах начальное значение плеча. Тогда g_∞(2)=0,295. Медианные значения V_∞/V₀ за 30-ти летний период приблизительно равны: для f=1: V_∞/V₀=288;для f=2: V_∞/V₀=6,974; для f=6,2: V_∞/V₀=2,86х10⁶. То есть разница в результатах при использовании плеча громадна за этот период. (примечание:Art Quaife сообщал о s=0,24 для периода 1980-1997. Читателю предлагается исследовать пример самостоятельно с этим изменением.)

Результаты раздела 3 непосредственно применимы к этой модели непрерывной аппроксимации портфеля ценных бумаг с (возможно) использованием кредитного плеча. Причиной тому – что обе модели подвержены воздействиям одинаковой динамики, а именно logG_n(f) аппроксимированное (шкалированное) Броуновским движением со смещением. Следовательно, мы можем ответить на тот же вопрос, на который мы отвечали при рассмотрении системы ставок в казино в разделе 3, но применительно к нашему портфелю. Например, (3.2) становится

где ^ означает знак возведения в степень, а 0<x<1. Используя (7.4), для r=0 и f=f ^*; 2 g_∞/Var(G_∞)=1, и это упрощается до

Сравним с Примером 3.3. При 0<r<m и f=f ^* показатель степени х в (7.9) становится 1+2rs²/(m-r)², а также имеет положительную первую производную, следовательно P(·) уменьшается с увеличением r (так как 0<x<1, стремится к 0 при стремлении r к m, что мы и ожидали).