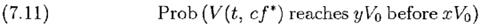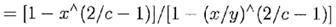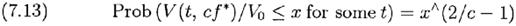D) Примечательная формула.

В ранних редакциях этой статьи показатель степени в уравнениях (3.2), (7.8) и (7.9) был без множителя 2, который я непреднамеренно пропустил при анализе. Впоследствии, 19 июня 1997 года Don Schlesinger опубликовал в интернете на сайте www.bjmath.com ещё две формулы общей непрерывной аппроксимации для случая r=0.

Если V₀ – начальный инвестиции и y>1>x>0, тогда для f ^* вероятность того, что V(t) достигнет yV₀ быстрее xV₀ будет

а с большей степенью общности, для f =сf ^*, 0<с<2

где ^ означает знак возведения в степень.

Очевидно, что (7.10) следует из (7.11) при выборе с=1. Случай r=0 для нашего уравнения (7.8) следует из (7.11), а тот же случай для уравнения (7.9) следует из (7.10). Мы можем получить обобщение (7.11) используя классическую формулу краха игрока (Cox and Miller, pp.205-6), где мы рассматриваем log(V(t, f)/V₀) как реализацию диффузного процесса со средним g_∞, дисперсией v(G_∞), начальным значением 0 и абсорбционными границами log y и log x. Результат будет

где a=2 g_∞/ V(G_∞)= 2M/V, M и V – сдвиг и дисперсия соответственно диффузного процесса на единицу времени. С другой стороны (7. 12) представляет собой иную запись известного решения для Винеровского процесса с двумя границами сдвига (Cox and Miller, Example 5.5).

Как отмечал Shlesinger, выбор x=1/2 и y=2 в (7.10) даёт Prob(V(t, f ^*) doubles before halving)=2/3. Рассмотрим теперь игрока или инвестора, который концентрирует внимание только на значениях V_n= 2ⁿ V₀, n=0, ±1, ±2,… кратное изменение его начального капитала.

В логарифмическом пространстве log(V_n/V₀)=n log2, то есть мы имеем случайное блуждание целыми множителями log2, где вероятность увеличения р=2/3, а уменьшения q=1/3. Это дает нам удобное наглядное и компактное представления уровня риска стратегии Кэлли.

Если же мы выберем с=1/2 («полукэлли»), уравнение (7.11) дает Prob(V(t, f ^*) doubles before halving)=8/9, что приводит к коэффициенту роста g_∞(f ^*/2)=0,75g_∞(f ^*), таким образом «полукэлли» имеет коэффициент роста равный 3/4f ^*, но гораздо меньший шанс потерпеть большие убытки.

Второе полезное наглядное сравнение риска вытекает из уравнения (7.8), которое даёт

Для с=1 мы имеем Prob(×)=x, а для с=1/2 мы получаем Prob(×)=x³. Следовательно «полукэлли» имеет значительно сниженную вероятность значительных потерь капитала. Шанс потери в какой-либо момент половины начального капитала составляет ½ для f =f ^*, но только 1/8 для f =f ^*/2. Мой опыт игры и инвестирования, так же как и сообщения от многочисленных игроков и команд блек-джека, говорит, что большинство людей почти всегда предпочитают безопасность роста и психологический комфорт «полукэлли» увеличению на четверть коэффициента роста.