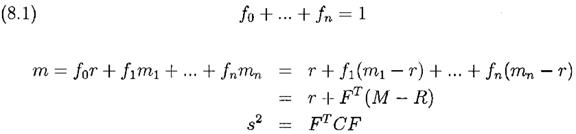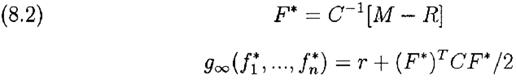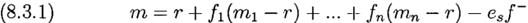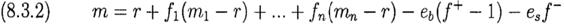D) Теория портфеля ценных бумаг.

Рассмотрим сперва неограниченный случай с безрисковой бумагой (казначейские векселя) с долей в портфеле f₀ и n ценными бумагами с долями в портфеле f₁,.., f_n. Предположим, что ставка доходности по безрисковому активу r, и, для простоты обсуждения, такое же значение примем для ставок заимствования, кредитования и ставки уплачиваемой при открытии коротких позиций. Пусть C=(s_ij)- ковариационная матрица с элементами s_ij, i, j=1,..,n представляющие собой ковариации между i и j бумагами, а M=(m₁,m₂,..m_n)^T вектор строка, такой что m_i, i=1,..,n будут уровни смещения i-ой бумаги.

Тогда портфель удовлетворяет соотношениям

где F^T=(f₁,..f_n) со знаком ^T означает транспонирование, а R – вектор-столбец (r,r,..r)^T длиной n.

Тогда наши предыдущие формулы и результаты для одной бумаги и одного безрискового актива приводят к g_¥(f₁,..f_n)=m-s²/2. Это стандартная задача оптимизации квадратичного программирования. Используя (8.1) и решая одновременные уравнения ∂g_¥/∂ f_i=0, i=1,..,n, мы получаем

где для удовлетворения требования единственности решения мы требуем существования С ^–1, то есть detC≠0. Когда все бумаги не коррелированны, то С диагональна и мы получаем f ^*=(m_i – r)/s_ii или f ^*=(m_i – r)/s_i², что соответствует (7.3) для n=1.

Примечание: BRK эмитировала новый тип непривилегированных акций с тикером BRK.B c одновременным изменением символа для старого типа на BRK.A. Одна акция BRK.A может быть конвертирована в 30 акций BRK.В в любое время, но не наоборот. Право голоса BRK.В имеет меньшее значение, а также отсутствуют право участия в назначении величины ежегодных благотворительных выплат. Мы вслед за рынком рассматриваем эти различия как незначительные, и согласно этому А торгуется по цене примерно в 30 раз превышающей котировку В.

Если бы отношение было всегда в точности 30 к 1, а также обе эти бумаги были бы включены в анализ, то они имели бы одинаковое значения ковариаций с другими бумагами, так что С=0 и C^-1 не существует.

Если существует ограничение на используемый маржинальный капитал с размером доли q, 0 ≤ q ≤ 1, тогда у нас появиться дополнительное ограничение

Подмножество с размерностью n замкнуто и ограничено.

Если ставка по заемным средствам для обеспечения портфеля r_b=r+e_b, e_b≥ 0, а ставка комиссии по коротким позициям r_s=r+e_s, e_s≥ 0, тогда m в уравнении (8.1) изменяется. Обозначим x⁺=max(x,0) а, x ^-=max(0,-x), так что x=x⁺- x ^– для всех x. Примем f ⁺=f₁⁺+…+f_n⁺ за долю портфеля размещенную в длинных позициях. И пусть f ^-=f₁^-+…+f_n^- - это доля портфеля размещенная в коротких позициях.

Случай 1. f ⁺≤ 1

Случай 2. f ⁺>1