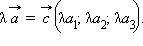| split capital investment trusts 363–4
| Tobin, J 356
|
| spot rates of exchange 237
| trading book model of capital adequacy 387
|
| spread betting 279
| transaction costs 12–14
|
| stakeholder products 340–1
| transaction exposure 262
|
| Standard and Poor’s 185
| translation exposure 262
|
| Stock Exchange Automated Quotation system
| Treaty on Economic and Monetary Union
|
| (SEAQ) 163
| (Maastricht Treaty) 252
|
| Stock Exchange Electronic Dealing System (SETS)
| trends in foreign exchange markets 250
|
|
| turnover 93
|
| stocks
|
|
| in nancial markets 22
| UK deposit insurance (2005) 58
|
| and ows 22, 35
| ultimate borrowers 23
|
| in household sector 36
| ultimate lenders 23
|
| straddle 281
| uncovered interest parity 242
|
| strangle 281
| uncovered interest rate arbitrage 243
|
| straps 281
| unfunded pension schemes 100–1
|
| strike price 273
| unit trusts 106–10
|
| strips 155
| prices and yields 108–9
|
| Summers, L H 54
| Unlisted Securities Market (USM)
|
| support levels in foreign exchange markets 250
|
|
| sustainable public debt 314
| variation margin 269
|
| swaps 301–5
| velocity of circulation 37–9
|
| swaptions 305
| venture capital trusts (VCTs) 333–4
|
| systemic risks 182–3, 387, 416–17
| vertical spreads 281
|
| tap stock 158
| warrants 278–9
|
| tap system 158
| whole of life policy 98
|
| taplets 158
| wholesale banking 62, 65
|
| taxation
| Wilson Committee 333
|
| of government bonds 160
| with prots insurance policy 98
|
| international, on capital movements 356–7
| without prots insurance policy 98
|
| of pension funds 105–6
|
|
| term structure of interest rates 221
| yield basis for certicates of deposit 122, 130
|
| expectations view of 223–8
| yield curve 221
|
| signicance of 229–31
| yield to maturity 152, 173–4
|
| time deposits 71
|
|
| time preference 205
| zero coupon swap 305
|
| time value of an option 277
|
|
Следствие 9.3.1.
Для того, чтобы точка C лежала на прямой AB, необходимо и достаточно, чтобы существовало такое число λ, что 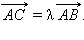
Следствие 9.3.2.
Для параллельности прямых AM и BN необходимо и достаточно, чтобы существовало такое число λ, что 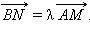
Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.
Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.

|
| Рисунок 9.2.1.
|
На рисунке 9.2.1 векторы 
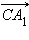 и
и  компланарны, так как, если отложить от точки C вектор
компланарны, так как, если отложить от точки C вектор  то все три вектора
то все три вектора 
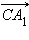 и
и  окажутся лежащими в одной плоскости. Векторы
окажутся лежащими в одной плоскости. Векторы 
 и
и  не компланарны, так как вектор
не компланарны, так как вектор  не лежит в плоскости ACD.
не лежит в плоскости ACD.
 Теорема 9.4. Теорема о разложении по базису в плоскости.
Теорема 9.4. Теорема о разложении по базису в плоскости.
Пусть векторы  и
и  не коллинеарны, тогда для любого вектора
не коллинеарны, тогда для любого вектора  лежащего в одной плоскости с
лежащего в одной плоскости с  и
и  существует единственная пара чисел α и β, такая, что
существует единственная пара чисел α и β, такая, что
Эта теорема верна и для того случая, когда векторы 
 и
и  параллельны одной плоскости.
параллельны одной плоскости.
 Теорема 9.5.
Теорема 9.5.
Если векторы 
 и
и  , отложенные от одной точки, не лежат в одной плоскости, то равенство
, отложенные от одной точки, не лежат в одной плоскости, то равенство
верно только при x = y = z = 0.
Эта теорема позволяет от одного векторного равенства переходить к системе числовых равенств.
 Теорема 9.6. Теорема о разложении по базису в пространстве.
Теорема 9.6. Теорема о разложении по базису в пространстве.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Эта теорема доказывается аналогично теореме 9.4, и поэтому мы не будем на ней подробно останавливаться.
Рассмотрим три взаимно перпендикулярные прямые x, y, z, пересекающиеся в одной точке O (чертеж 9.3.1).
|
|
| Чертеж 9.3.1.
Декартовы координаты в пространстве.
|
Проведем через каждую пару этих прямых плоскость. Плоскость, проходящая через прямые x и y, называется плоскостью xy. Две другие плоскости называются, соответственно, плоскостями xz и yz.
 Определение 9.11.
Определение 9.11.
Прямые x, y, z называются координатными осями (или осями координат), точка их пересечения O – началом координат, а плоскости xy, xz и yz – координатными плоскостями. Точка O разбивает каждую координатную ось на две полупрямые, которые называются положительной и отрицательной полуосями.
Рассмотрим теперь произвольную точку A и проведем через нее плоскость, параллельную плоскости yz (чертеж 9.3.2).
|
|
| Чертеж 9.3.2.
Координаты точки.
|
Пусть эта плоскость пересекает ось x в некоторой точке Ax.
 Определение 9.12.
Определение 9.12.
Координатой точки A по оси x будем называть число, равное по абсолютной величине длине отрезка OAx: положительное, если точка A лежит на положительной полуоси x, и отрицательное, если она лежит на отрицательной полуоси.
Если же точка Ax совпадет точкой O, то полагаем по определению, что x = 0. Аналогично можно определить координаты y и z точки A. Координаты точки A записываются в скобках рядом с названием этой точки: A (x; y; z).
Зададим теперь в пространстве прямоугольную систему координат.
 Определение 9.13.
Определение 9.13.
Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный вектор, направленный вдоль оси x, обозначается  единичный вектор, направленный вдоль оси y –
единичный вектор, направленный вдоль оси y –  вдоль оси z –
вдоль оси z –  Вектора
Вектора 

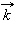 называются координатными векторами.
называются координатными векторами.
любой вектор  можно разложить по координатным векторам:
можно разложить по координатным векторам:
Кроме того, отметим, что по уже доказанному коэффициенты разложения определяются единственным образом. Эти коэффициенты и называются координатами вектора  в данной системе координат.
в данной системе координат.
Следующие утверждения доказываются аналогично их планиметрическим аналогам.
- Координаты нулевого вектора равны нулю.
- Координаты равных векторов соответственно равны.
Пусть 
 тогда
тогда 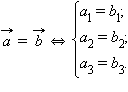
- Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.
Пусть 
 тогда
тогда 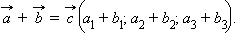
- Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.
Пусть 
 тогда
тогда 
- Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.
Пусть 
 тогда
тогда 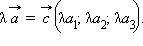

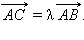
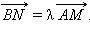


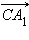 и
и  компланарны, так как, если отложить от точки C вектор
компланарны, так как, если отложить от точки C вектор  то все три вектора
то все три вектора  окажутся лежащими в одной плоскости. Векторы
окажутся лежащими в одной плоскости. Векторы 
 и
и  Теорема 9.4. Теорема о разложении по базису в плоскости.
Теорема 9.4. Теорема о разложении по базису в плоскости. и
и  не коллинеарны, тогда для любого вектора
не коллинеарны, тогда для любого вектора  лежащего в одной плоскости с
лежащего в одной плоскости с  существует единственная пара чисел α и β, такая, что
существует единственная пара чисел α и β, такая, что

 параллельны одной плоскости.
параллельны одной плоскости.

 Определение 9.11.
Определение 9.11.
 единичный вектор, направленный вдоль оси y –
единичный вектор, направленный вдоль оси y –  вдоль оси z –
вдоль оси z –  Вектора
Вектора 

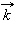 называются координатными векторами.
называются координатными векторами.

 тогда
тогда 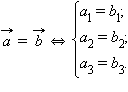
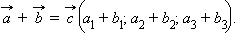

 тогда
тогда