 Определение 3.8.
Определение 3.8.
Двугранный угол – это часть пространства, заключенная между двумя полуплоскостями, имеющими одну общую границу.
Полуплоскости α и β, образующие двугранный угол, называются его гранями (чертеж 3.6.1). Общая прямая этих граней называется ребром двугранного угла. Пусть точки A и B взяты на ребре двугранного угла. Двугранный угол обозначается двумя буквами: угол AB. Иногда двугранный угол обозначается четырьмя буквами, из которых две средних обозначают точки ребра, а две крайние – точки, взятые на гранях. Пусть M  α, N
α, N  β (чертеж 3.6.1), тогда двугранный угол обозначается так: угол MABN. Выберем на ребре AP двугранного угла произвольную точку C и проведем через нее плоскость αперпендикулярно ребру AP (чертеж 3.6.2). Плоскость α пересекает грани двугранного угла по лучам a и b, которые образуют некоторый угол величиной φ. Этот угол называется линейным углом двугранного угла. Легко доказать, что величина линейного угла не зависит от выбора точки C на ребре AP. Возьмем на ребре AP точку D, отличную от C, и проведем через нее плоскость β || α. Пусть плоскость β пересекает грани двугранного угла по лучам a 1 и b 1. Согласно теореме о следе a 1 || a, b 1 || b, поэтому полученные в сечении углы равны. Величина двугранного угла равна величине его линейного угла. Если φ – величина двугранного угла, то 0° < φ < 180°.
β (чертеж 3.6.1), тогда двугранный угол обозначается так: угол MABN. Выберем на ребре AP двугранного угла произвольную точку C и проведем через нее плоскость αперпендикулярно ребру AP (чертеж 3.6.2). Плоскость α пересекает грани двугранного угла по лучам a и b, которые образуют некоторый угол величиной φ. Этот угол называется линейным углом двугранного угла. Легко доказать, что величина линейного угла не зависит от выбора точки C на ребре AP. Возьмем на ребре AP точку D, отличную от C, и проведем через нее плоскость β || α. Пусть плоскость β пересекает грани двугранного угла по лучам a 1 и b 1. Согласно теореме о следе a 1 || a, b 1 || b, поэтому полученные в сечении углы равны. Величина двугранного угла равна величине его линейного угла. Если φ – величина двугранного угла, то 0° < φ < 180°.
 Определение 3.9.
Определение 3.9.
1. При пересечении двух плоскостей образуются четыре двугранных угла. Величина меньшего из этих двугранных углов называется углом между этими плоскостями.
Если плоскости параллельны, то угол между ними равен 0° по определению. Если φ – величина угла между двумя плоскостями, то 0° < φ < 90°.

 Определение 3.8.
Определение 3.8.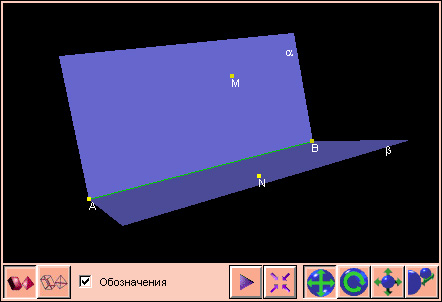
 α, N
α, N 



