Расстояние между точками
Рассмотрим точки A 1 (x 1; y 1; z 1) и A 2 (x 2; y 2; z 2) и найдем расстояние между этими точками.
Расстояние между точками A 1 и A 2 можно вычислить по формуле
Вектор, конец которого совпадает с данной точкой, называется радиус-вектором данной точки. Рассмотрим некоторую точку M в пространстве с координатами (x; y; z). Пусть M 1, M 2, M 3 – точки пересечения с осями координат плоскостей, проходящих через точку M перпендикулярно к этим осям (чертеж 9.4.2). Тогда
По определению координаты точки M
Координаты любой точки равны соответствующим координатам ее радиус-вектора. Рассмотрим теперь две точки
Эта формула позволяет вычислять длину вектора, зная его координаты.
Рассмотрим два произвольных вектора:
Ненулевой вектор называется направляющим вектором прямой a, если он лежит либо на прямой a, либо на прямой, параллельной a.
Углом между ненулевыми векторами называется угол между прямыми, для которых данные вектора являются направляющими. Угол между любым вектором и нулевым вектором по определению считаем равным нулю. Если угол между векторами равен 90°, то такие вектора называются перпендикулярными. Угол между векторами будем обозначать так:
Скалярным произведением векторов
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:
Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим. Для любых векторов
|

 Теорема 9.7.
Теорема 9.7.
 Определение 9.14.
Определение 9.14.
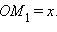 Значит,
Значит,  Совершенно аналогично
Совершенно аналогично 
 Получается, что
Получается, что  Тем самым доказана следующая
Тем самым доказана следующая и
и  По только что доказанному,
По только что доказанному,  Итак, каждая координата вектора равна разности соответствующих координат его конца и начала. Но длина вектора
Итак, каждая координата вектора равна разности соответствующих координат его конца и начала. Но длина вектора  по определению равна длине отрезка
по определению равна длине отрезка  а длина этого отрезка есть расстояние между точками
а длина этого отрезка есть расстояние между точками  и
и  Значит,
Значит,
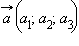 и
и 
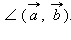
 и
и  называется произведение их длин на косинус угла между ними:
называется произведение их длин на косинус угла между ними:
 заданных своими координатами, может быть вычислено по формуле
заданных своими координатами, может быть вычислено по формуле 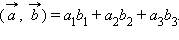

 и
и  и любого числа λ справедливы равенства:
и любого числа λ справедливы равенства: причем
причем 
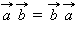 (переместительный закон).
(переместительный закон).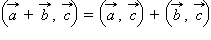 (распределительный закон).
(распределительный закон). (сочетательный закон).
(сочетательный закон).


