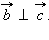Перпендикулярность прямой и плоскости
Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости. Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.
Две прямые, перпендикулярные одной плоскости, параллельны между собой.
Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.
Две плоскости, перпендикулярные одной прямой, параллельны между собой. Докажите эти теоремы самостоятельно, используя такое свойство: если векторы
Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной данной плоскости, который соединяет данную точку с точкой плоскости.
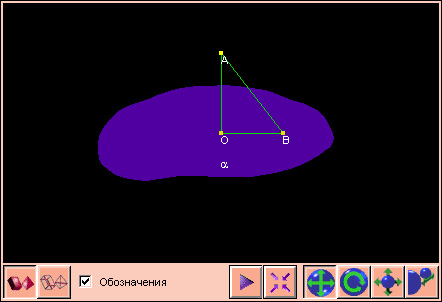
Пусть AO – перпендикуляр к плоскости α (чертеж 3.2.4), O – основание перпендикуляра. Длина этого перпендикуляра AO называется расстоянием от точки A до плоскости α;. Отрезок, соединяющий точку A с любой точкой плоскости, отличной от O, называется наклонной (AB – наклонная, B – основание наклонной, BO – проекция наклонной на плоскость α, то есть BO = Прα AB).
Если из одной точки вне плоскости проведены к ней перпендикуляр и наклонные, то
Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость.
|

 Определение 3.3.
Определение 3.3. Теорема 3.1. Признак перпендикулярности прямой и плоскости.
Теорема 3.1. Признак перпендикулярности прямой и плоскости.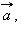
 коллинеарные и
коллинеарные и  то
то