Поділ кола і побудова правильних багатокутників

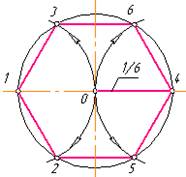
3.6.1. Поділ кола на 3, 6, 12 рівних частин.

3.6.1.1. Щоб поділити коло на три однакові частини і вписати в нього правильний трикутник, з точки перетину центрової лінії з колом, як із центра, проводять додаткову дугу радіусом, що дорівнює радіусу R кола (рис. 3.11а). Одержують точки 1 і 2. Точки 1, 2, 3 поділяють коло на три однакові частини. З’єднавши прямими лініями точки 1, 2, 3 отримують правильний трикутник (рис. 3.11б).

а	б	в
Рис. 3.11. Поділ кола на 3, 6 рівних частин

3.6.1.2. Щоб поділити коло на шість рівних частин, з двох протилежних точок перетину центрової лінії з колом 1 і 4 описують дві дуги радіусом, що дорівнює радіусу R кола. Отримують точки 2, 3, 5, 6. Разом з точками 1 і 4 вони ділять коло на шість рівних частин. З’єднують прямими лініями точки 1…6 і отримують правильний вписаний шестикутник (рис. 3.11в).

3.6.1.3. Поділ кола на дванадцять рівних частин виконують аналогічно. З кінців взаємно перпендикулярних діаметрів кола, як із центрів, проводять дуги тим же радіусом, що й у кола. Одержані точки перетину дуг з колом і будуть вершинами правильного дванадцятикутника.

3.6.2. Поділ кола на 4 і 8 рівних частин.

3.6.2.1. Два взаємно перпендикулярних діаметра перетинають коло в точках 1, 2, 3, 4, які ділять коло на чотири рівні частини. З’єднують прямими лініями точки 1…4 і отримують правильний вписаний чотирикутник (рис. 3.12а).

На рисунку 3.12б показано, як ділять коло на чотири частини за допомогою бісектриси прямого кута. Ділять прямий кут в колі навпіл (див. п.3.3.1.). Пряма О5 і О8 (бісектриси кута)перетинають коло в точках 6 і 7, 9 і 10, що ділять коло на чотири рівні частини.

а	б	в
Рис. 3.12. Поділ кола на 4, 8 рівних частин

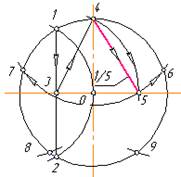
3.6.2.2. На основі двох наведених способів поділу кола на чотири рівні частини ділять коло на вісім рівних частин і вписують в нього правильний восьмикутник (рис. 3.12в).

3.6.3. Поділ кола на 5 і 10 рівних частин.

З точки перетину центрової лінії з колом, як із центра, проводять додаткову дугу радіусом, що дорівнює радіусу R кола (рис.3.13а). Одержують точки 1 і 2. Хорда 12 ділить радіус кола точкою 3 навпіл. З точки 3, як із центра, описують дугу радіусом 34 до перетину з горизонтальним діаметром колав точці 5. Відрізок 45 дорівнює стороні правильного п’ятикутника. Відклавши відрізок 45, як хорду, вздовж кола отримують точки 4, 6, 9, 8, 7, які є вершинами правильного вписаного п’ятикутника (рис.3.13б).

Відрізок 27 дорівнює стороні правильного десятикутника (рис. 3.13в).

а	б	в
Рис. 3.13. Поділ кола на 5, 10 рівних частин

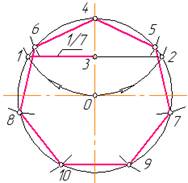
3.6.4. Поділ кола на 7 рівних частин.

Щоб поділити коло на сім однакових частин з точки перетину

Рис. 3.14. Поділ кола на 7 рівних частин

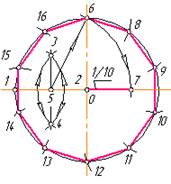
центрової лінії з колом, як із центра, проводять додаткову дугу радіусом, що дорівнює радіусу R кола. Одержані точки перетину цієї дуги з колом 1 і 2 з’єднують прямою лінією. Половина хорди 12 відрізок 13 дорівнює стороні правильного вписаного семикутника (рис. 3.14).

3.6.5. Поділ кола на п рівних частин.

В заданому колі проводять два взаємно перпендикулярних діаметра і вертикальний діаметр CD ділять на п рівних частин, наприклад на дев’ять (рис. 3.15). З точки С, як із центра, радіусом R, який

Рис. 3.15. Поділ кола на п рівних частин

дорівнює діаметру кола, описують дугу. Місця перетину цієї дуги з горизонтальною віссю позначають точками А і В. З цих точок проводять прямі через парні або непарні поділки вертикального діаметру CD до перетину з колом. Одержані точки поділять коло на п рівних частин (на дев’ять). З’єднують ці точки і отримують правильний багатокутник.