Нанесення розмірів на креслениках
2.6.1. Загальні відомості. Розміри на креслениках наносять за вимогами ГОСТ 2.307-68 «Нанесение размеров и предельных отклонений». Розміри розподіляють на лінійні і кутові. Лінійні наносять в міліметрах без зазначення одиниць виміру, а кутові– в градусах, хвилинах і секундах із зазначенням одиниць виміру (рис. 2.13). Кожен розмір на кресленику наносять тільки один раз. Загальна кількість розмірів на кресленику виробу повинна бути мінімальною, але достатньою для виготовлення виробу за його креслеником. 2.6.2. Розмірні та виносні лінії. Розмірні та виносні лінії креслять суцільними тонкими лініями, товщиною 0,2-0,3 мм. Розмірні лінії проводять паралельно до відрізку і такої ж довжини, а виносні лінії - перпендикулярно до розмірних (рис. 2.13а,б). Рекомендують виносити розмірні лінії за контур зображення деталі. Слід уникати перетину розмірних та виносних ліній іншими лініями. Для цього, ближче до контуру зображення, проводять розмірні лінії меншого
розміру, а далі від контуру – розмірні лінії більшого розміру. Мінімальна відстань між контуром зображення і розмірною лінією – 10 мм, між паралельними розмірними лініями – 7 мм (рис. 2.13а,б).
При нанесенні розміру кута розмірну лінію проводять у вигляді дуги кола з центром у вершині кута, а виносні лінії йдуть радіально (рис. 2.13в). На деталі з розривом розмірну лінію проводять між крайніми точками і проставляють розмір всієї її довжини (рис. 2.14а). На деталі з обривом, розмірну лінію заводять за вісь і проставляють довжину всієї деталі (рис. 2.14б).
При з’єднанні зображення виду та розрізу симетричного виробу,
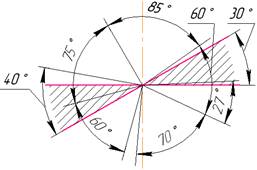
розмірну лінію проводять з обривом трохи далі вісі й проставляють весь діаметр або всю довжину. Розміри, які відносять до розрізу, проставляють зі сторони розрізу. Розміри, які відносять до виду – зі сторони виду (рис. 2.15). 2.6.3. Розмірні числа. Розміри на кресленику показують розмірними числами, які відповідають дійсним розмірам виробу, незалежно від масштабу його зображення. Висота розмірних чисел – 3,5 мм. Їх наносять над горизонтальною розмірною лінією ближче до середини. На вертикальних розмірних лініях розмірні числа розташовують зліва від розмірної лінії. Розмірні числа лінійних розмірів при різних нахилах розмірних ліній розміщують як приведено на рисунку 2.16а. Лінійні розміри, які при нахилах розмірних ліній до вертикалі менше 30º (заштрихована зона) наносять на поличках ліній-виносок (рис. 2.16б). Якщо над розмірною лінією недостатньо місця для написання розмірного числа, то розміри наносять як показано на рисунку 2.17.
При декількох паралельних або концентричних розмірних лініях розмірні числа розташовують у шаховому порядку (рис. 2.18).
2.6.4. Радіуси та діаметри. При нанесенні розміру радіусу перед розмірним числом пишуть велику літеру R, а розмірну лінію проводять із центру дуги. Розмірні лінії
двох радіусів, проведених з одного центру, не розташовують на одній прямій (рис. 2.19а). Нанесення розмірів радіусів зовнішніх та внутрішніх заокруглень показано на рисунку 2.19б. Перед розмірним числом діаметру наносять знак ∅, розмірну лінію проводять через центр кола або паралельно будь-якій осі (рис. 2.20а). При неповному зображенні кола розмірну лінію діаметру обривають за центром (рис. 2.20б).
При малих розмірах діаметрів розмірні числа та стрілки на розмірних лініях наносять зовні кола (рис. 2.20в). В таких випадках центрові лінії кола виконують не штрихпунктирною тонкою лінією, а тонкою суцільною. Якщо виріб має декілька однакових отворів, то на поличці лінії-виноски вказують діаметр одного отвору та їх кількість (рис. 2.21).
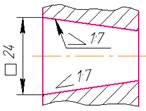
2.6.5.Розміри фасок. Розміри фасок під кутом 45° наносять відповідно рисунку 2.22а.
Розміри фасок під іншими кутами позначають за загальними правилами – лінійними і кутовими розмірами або двома лінійними розмірами (рис. 2.22б). 2.6.6. Похил і конусність. Похил - це величина, яка характеризує нахил однієї лінії відносно іншої. Похил лінії визначається тангенсом кута її нахилу, тобто відношенням протилежного катету до прилеглого. Розмірне число похилу вказують у відсотках (рис. 2.23а) або у вигляді співвідношення (рис. 2.23б), а перед розмірним числом наносять знак Конусність поверхні конуса – це відношення діаметру конуса до його висоти або відношення різниці діаметрів зрізаного конуса до його висоти. Розмірне число конусності вказують відношенням, перед яким наносять знак
3. Найпростіші геометро-графічні побудови 3.1. Побудова паралельних і перпендикулярних прямих 3.1.1. Побудова паралельних прямих. 3.1.1.1. Побудова прямої в паралельної до прямоїа через задану точку С, що не лежить на цій прямій. Перший спосіб. На прямій а від точки А відкладають довільний відрізок АВ (рис. 3.1а). Проводять дуги: з точки С радіусом R=АВ та з точки В радіусом R=АС. Пряма, що проходить через точку С і точку D
перетину проведених дуг, буде паралельною до заданої прямої а. Другий спосіб. На відрізку АВ прямої а вибирають довільну точку О (рис. 3.1б). З цієї точки, як із центра, описують дугу радіусом R=ОС до перетину з відрізком АВ в точках К і Е. З точки К дугою радіусом R=СЕ роблять засічку на першій дузі і одержують точку D. Пряма в, проведена через точки D і С, є шуканою прямою, паралельною до відрізку АВ. 3.1.1.2. Побудова паралельної прямої на заданій відстані R. З двох точок, довільно взятих на заданому відрізку АВ, описують дві допоміжні дуги радіусом R, який дорівнює відстані між паралельними прямими (рис. 3.1в). Далі проводять спільну дотичну до дуг в, яка буде паралельною до заданого відрізку АВ і віддаленою від нього на відстань R. 3.1.2. Побудова перпендикулярних прямих. 3.1.2.1. Побудова перпендикуляра в до прямої а з точки С, яка лежить поза прямою. З точки С проводять дугу довільного радіусу до перетину з заданою прямою а в точках 1 і 2 (рис. 3.2а). З отриманих точок описують дуги довільного радіусу до їх перетину в точці 3. Пряма в проведена через точки С і 3 є шуканим перпендикуляром.
3.1.2.2. Побудова перпендикуляра в до прямої а, що проходить через її кінцеву точку А. З довільно вибраної точки 1 (рис. 3.2б), що лежить поза прямою а описують дугу кола радіусом R=1А, яка перетинає задану пряму а в точці 2. Проводять діаметр через точки 1 і 2 до перетину з колом в точці 3. Пряма А3 перпендикулярна до заданої прямої а, оскільки кут 2А3 – вписаний і опирається на діаметр, а тому дорівнює 90°. 3.1.2.3. Побудова перпендикуляра в до прямої а з точки А, що лежить на прямій а. З заданої точки А на прямій а описують дугу довільного радіусу R до перетину з заданою прямою в точках 1 і 2 (рис. 3.2в). З одержаних точок описують дуги довільного радіусу R1 більшого ніж попередній R1>R. Пряма, що проходить через точку А і точку 3 перетину дуг радіусу R1, перпендикулярна до заданої прямої а.
|






















 , вершина якого спрямована в бік похилу.
, вершина якого спрямована в бік похилу.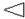 , вершина якого направлена в бік вершини конуса (рис. 2.23в).
, вершина якого направлена в бік вершини конуса (рис. 2.23в).