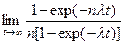Исследование функции риска

 

Предполагая, что все элементы системы имеют равную надежность, а интенсивность отказа каждого элемента λ;= λ_с/n =9,210^-5/8=1,1510^-5 час^-1, получить выражение для риска системы по формуле 7.3 в зависимости от n и t.

Найти зависимость R_c(t) при различных значениях n в виде графиков и таблиц, используя возможности пакета Excel.

Примечание:Основной задачей исследования функции риска является определение влияния числа элементов системы на динамику изменения риска с наработкой. Поэтому расчеты проводятся для одного и того же значения среднего риска, соответствующего среднему риску заданной системы при равнонадежных элементах:

.

Получение графика функции риска

Построить график функции риска, выполнив для этого следующие действия:

1.Сформировать вектор {ni}, состоящий из значений, определяющих количество элементов в системе (n =8; 24; 40).

2.Сформировать вектор { t_i }, состоящий из дискретных значений времени:

3.Вычислить значения функции риска для значений времени при n =8.

Для этого ввести в ячейку выражение для риска R_c(t,n)

=3300*(1-EXP(-1,15*0,00001*$B$15*B17))

В результате получится вектор значений функции риска:

0,00

148,36

234,16

290,05

1216,76

1984,89

2775,90

3091,14

3216,76

3266,83

3286,78

4.Аналогично вычислить значения функции риска при n =24 и n =40. В результате получатся два вектора:

0,00	425,37	653,81	795,92	2469,79	3091,14	3286,78	3299,16	3299,95	3300,00	3300,00
0,00	678,04	1016,01	1216,76	2969,15	3266,83	3299,67	3300,00	3300,00	3300,00	3300,00

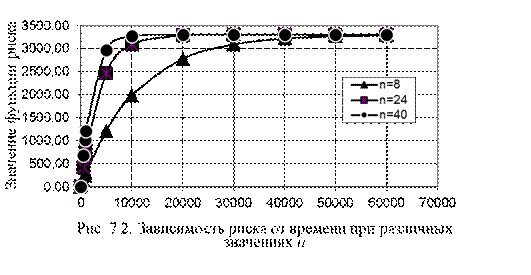
5.Выделить необходимые для построения данные – значения времени и функции риска при разном количестве элементов системы.

6.Выбрать на панели инструментов пиктограмму «Мастер диаграмм». Выбрать тип диаграммы – точечная. Нажать кнопку «Далее». На вкладке «Диапазон данных» выбрать: «Ряды в: строках». На вкладке «Ряд» задать названия рядов: n =8, n =24, n =40. Нажать кнопку «Далее». На вкладке «Заголовки» в строке «Название диаграммы» ввести «Зависимость функции риска от количества элементов и времени», ось Х назвать «Время», а ось Y – «Значение функции риска». На вкладке «Легенда» выбрать: «Добавить легенду. Размещение – справа». Нажать кнопку «Далее», а затем кнопку «Готово».

7.Результат приведен на рис. 7.2.

Из графика видно, что с увеличением времени t работы системы техногенный риск функционирования системы увеличивается и при t →∞ стремится к постоянной величине, равной среднему значению риска системы.

 

7.4.4. Исследование зависимости G_R(t,n)

 

Для анализа зависимости G_R(t,n) представим эту функцию в виде таблиц и графиков. Графики позволяют сделать качественный анализ, а таблицы – количественный.

 

Построение графиков G_R(t,n)

Предположим, что система состоит из n равнонадежных элементов, каждый из которых имеет интенсивность отказов λ;. Тогда функция G_R(t,n) будет выражаться формулой (6.5). Подставим в эту формулу значение λ;=1,15·10^-5 час^-1.

Построим графики для трех значений n: n, 3 n, 5 n, где n =8 – число элементов системы. Для построения графиков необходимо выполнить следующие действия:

1.Сформировать вектор { n_i }, состоящий из значений, определяющих количество элементов в системе (n =8;24;40).

2.Сформировать вектор { t_i }, состоящий из дискретных значений времени:

Значение времени t =0 не используется, так как в этом случае знаменатель дроби обращается в нуль.

3.Ввести в ячейку выражение для G_R(t,n):

=(1-EXP(-$B$15*1,15*0,00001*В51))/($B$15*(1-EXP(-1,15*0,00001*В51)))

(в ячейке B15 – количество элементов системы n =8, а в ячейке В51 – значение времени t =1).

В результате получится значение функции G_R (1,8)=1,00.

4.Вычислить значение функции G_R (t,8) для других значений времени при n =8. В результате получится вектор значений функции G_R (t,8):

5.Аналогично вычислить значения функции G_R(t,n) при n =24 и n =40. В результате получатся два вектора:

6.Для построения графиков необходимо выполнить пп. 6-8 раздела 7.4.3. График приведен на рис. 7.3.

В итоге мы получили семейство кривых, из которых можно сделать два важных вывода:

1. Чем больше элементов n и чем больше время работы системы, тем больше погрешность приближенной формулы.

2. Приближенной формулой можно пользоваться в том случае, когда время работы системы мало и риск, вычисленный по приближенной формуле, не превышает допустимого значения.

Функция G_R(t,n) является убывающей. Это означает, что с увеличением времени и увеличением числа элементов погрешность приближенной формулы возрастает. Определим предельные значения функции G_R(t,n). Пределы существуют, если переменные n и λ; положительные и значение n конечно. В этом случае, находя предел функции G_R(t,n), мы получаем следующий выражение:

При t→∞ экспоненты и в числителе, и в знаменателе будут стремиться к нулю. Поэтому в пределе получим значение 1/n. Таким образом, предельное значение функции G_R(t,n) = 1/n.
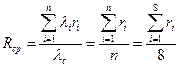